Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 12. 2017 20:06
Hessián - nutná a postačující podmínka
Ahoj,
není mi úplně jasná otázka :
Mějme funkci f : R^n → R mající spojité všechny druhé parciální derivace. Které z následujících tvrzení je postačující podmínkou pro existenci lokálního minima funkce f v bodě a ?
a) Ani jedna z uvedených možností
b) 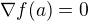 a
a  pro každé
pro každé 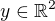
c) 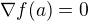 a
a  pro každé nenulové
pro každé nenulové 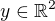
d) 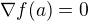 a
a  pro každé nenulové
pro každé nenulové 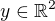
e) 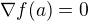 a
a  pro každé nenulové
pro každé nenulové 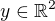
Správná odpověď má být C, má to něco k dočinění s rozdílem nutné a postačující podmínky, ale já to v tom bohužel nevidím :/ Mohl bych poprosit o objasnění ?
Díky
Offline
#2 28. 12. 2017 20:28
Re: Hessián - nutná a postačující podmínka
↑ Archer785:
Ahoj
Zkus popřemýšlet o aproximaci funkce Taylorovým polynomem a o vlastnostech kvadratických forem.
Offline
