Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Transformace členů sumy na konvergentní sumu (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 07. 2010 22:23
- check_drummer

- Příspěvky: 4946
- Reputace: 106
Transformace členů sumy na konvergentní sumu
Ahoj,
mějme posloupnost  splňující:
splňující:
a)  jsou kladná reálná čísla
jsou kladná reálná čísla
b) 
Dokažte nebo vyvraťte následující dvě tvrzení:
1) Pro každou posloupnost  splňující výše uvedené body a), b) existuje ostře rostoucí funkce f z
splňující výše uvedené body a), b) existuje ostře rostoucí funkce f z  do
do  , že
, že 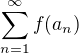 konverguje.
konverguje.
2) (silnější tvrzení, funkce nezávisí na definici posloupnosti): Existuje ostře rostoucí funkce f z  do
do  , že pro každou posloupnost
, že pro každou posloupnost  splňující výše uvedené body a), b) platí:
splňující výše uvedené body a), b) platí: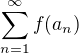 konverguje.
konverguje.
(Pozor, v obou případech f nezávisí na indexu prvku posloupnosti.)
Řešení neznám, úloha mě napadla dnes.
"Máte úhel beta." "No to nemám."
Online
- (téma jako vyřešené označil(a) check_drummer)
#2 12. 07. 2010 23:50 — Editoval BrozekP (12. 07. 2010 23:57)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Transformace členů sumy na konvergentní sumu
Offline
#3 13. 07. 2010 00:01 — Editoval Olin (13. 07. 2010 00:04)
Re: Transformace členů sumy na konvergentní sumu
Offline
#5 13. 07. 2010 09:10 — Editoval Rumburak (13. 07. 2010 09:15)
Re: Transformace členů sumy na konvergentní sumu
↑ jarrro:
Z elegantního a přehledného důkazu podaného v příslušné části příspěvku od kolegy Brožka ↑ BrozekP: jsem si odnesl názor,
že zde žádné přidané předpoklady kladené na funkci f nepomohou.
Offline
#6 13. 07. 2010 10:16
Re: Transformace členů sumy na konvergentní sumu
↑ Rumburak:myslel som skôr na postupnosť a_n,že nie len nulová limita a kladné,ale niečo silnejšie
MATH IS THE BEST!!!
Offline
#7 13. 07. 2010 10:54 — Editoval Rumburak (13. 07. 2010 13:09)
Re: Transformace členů sumy na konvergentní sumu
↑ BrozekP: na vědomí ↑ jarrro:
Ahoj,
dodatečně si uvědomuji, že v Tvém důkazu bodu 2, který se mi na první pohled tolik líbil, je bohužel zádrhel:
Offline
#8 13. 07. 2010 11:10
Re: Transformace členů sumy na konvergentní sumu
↑ Rumburak:Olin to obišiel čiže taká funkcia neexistuje,ale nedá sa pridať nejaký ďalší predpoklad o a_n okrem nulovej limity a kladnosti,aby taká funkcia pre postupnosti spĺňajúce tie podmienky existovala?
MATH IS THE BEST!!!
Offline
#10 13. 07. 2010 13:40
Re: Transformace členů sumy na konvergentní sumu
Tak si to zkusme docela dost oslabené:
Rozhodněte, zda existuje rostoucí funkce 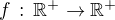 taková, že řada
taková, že řada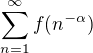
konverguje pro každé  .
.
Offline
#11 13. 07. 2010 21:47
#12 14. 07. 2010 19:46
- check_drummer

- Příspěvky: 4946
- Reputace: 106
Re: Transformace členů sumy na konvergentní sumu
↑ Rumburak:
Co např. technicky dodefinovat  ve "zlobivých" bodech jako
ve "zlobivých" bodech jako  pro nějaké "dostatečně malé" d (dx zde neznamená znak diference)?
pro nějaké "dostatečně malé" d (dx zde neznamená znak diference)?
S tím souvisí ještě jedna věc, že je nutné ukázat (a toho jsem si výše nevšiml, že by k tomu došlo), že platí 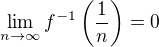 , což by díky vlastnosti f: bodu b) a nutné konvergence sumy plus díky volbě
, což by díky vlastnosti f: bodu b) a nutné konvergence sumy plus díky volbě  mělo platit (důkaz však nepodávám).
mělo platit (důkaz však nepodávám).
"Máte úhel beta." "No to nemám."
Online
#13 14. 07. 2010 20:30
Re: Transformace členů sumy na konvergentní sumu
ak tá funkcia splňuje podmienku tak rad 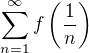 konverguje teda je
konverguje teda je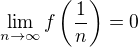 teda aj
teda aj 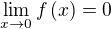 grafy inverzných funkcií sú súmerne združené podľa y=x teda musí byť aj
grafy inverzných funkcií sú súmerne združené podľa y=x teda musí byť aj 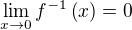 teda aj
teda aj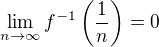 nezaručujem správnosť
nezaručujem správnosť
MATH IS THE BEST!!!
Offline
#14 22. 07. 2010 16:07 — Editoval Marian (22. 07. 2010 16:08)
Re: Transformace členů sumy na konvergentní sumu
Nejprve uvedu jednu definici a potom větu, která je známa a mohla by se hodit k diskutovanému tématu.
______________________________
Definice (zachovávání konvergence nekonečné řady). Funkce 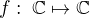 zachovává konvergenci řady
zachovává konvergenci řady 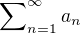 , jestliže pro každou konvergentní řadu
, jestliže pro každou konvergentní řadu 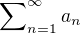 s komplexními členy její transformace
s komplexními členy její transformace 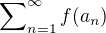 konverguje.
konverguje.
______________________________
A nyní slibované tvrzení ...
______________________________
Věta. (A) Funkce 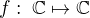 zachovává konvergenci řady tehdy a jen tehdy, jestliže je spojitá v jistém sférickém okolí bodu
zachovává konvergenci řady tehdy a jen tehdy, jestliže je spojitá v jistém sférickém okolí bodu 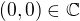 a existuje takové
a existuje takové  , že platí:
, že platí:
(i) jestliže  ,
,  ,
,  , potom
, potom 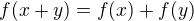 ;
;
(ii) jestliže  a
a  , potom
, potom 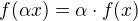 .
.
(B) Funkce 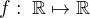 zachovává konvergenci řady tehdy a jen tehdy, jestliže existuje takové
zachovává konvergenci řady tehdy a jen tehdy, jestliže existuje takové  a
a 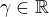 , že pro všechna
, že pro všechna 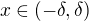 platí
platí 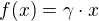 (tedy
(tedy  je lineární v nějakém okolí bodu
je lineární v nějakém okolí bodu 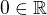 ).
).
______________________________
Větu lze nalézt v knize Šalát Tibor. Nekonečné rady. Academia, Praha 1974. na stránkách 84 a 85. Důkaz tvrzení je v téže knize na stránkách 85, 86 a 87.
Offline
#15 23. 07. 2010 06:43
Re: Transformace členů sumy na konvergentní sumu
Dokážete uvést příklad takové řady, že
konverguje, ale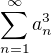
diverguje?
Pár poznatků, co musí řada splňovat:
Offline
#16 23. 07. 2010 08:50
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Transformace členů sumy na konvergentní sumu (TOTO TÉMA JE VYŘEŠENÉ)
 a rekurzivně
a rekurzivně  (
(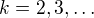 ) taková
) taková  , že
, že 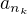 je maximem posloupnosti
je maximem posloupnosti 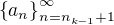 (takové
(takové  existovat, protože limita
existovat, protože limita 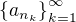 je zřejmě klesající. Definujme nyní funkci
je zřejmě klesající. Definujme nyní funkci 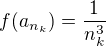 . Na zbytku definičního oboru ji definujme libovolně tak, aby splňovala podmínky zadání.
. Na zbytku definičního oboru ji definujme libovolně tak, aby splňovala podmínky zadání.
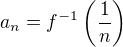 .
.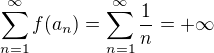
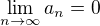 a jde o posloupnost kladných čísel, jedna konkrétní hodnota se v posloupnosti
a jde o posloupnost kladných čísel, jedna konkrétní hodnota se v posloupnosti 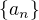 může vyskytnout pouze na konečně mnoha místech. Nechť se
může vyskytnout pouze na konečně mnoha místech. Nechť se 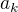 vyskytne v posloupnosti
vyskytne v posloupnosti 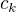 místech a nechť je to v této posloupnosti
místech a nechť je to v této posloupnosti  -té největší číslo (myšleno tak, že když je tam jedno číslo vícekrát, tak se počítá pouze jednou). Označme ještě
-té největší číslo (myšleno tak, že když je tam jedno číslo vícekrát, tak se počítá pouze jednou). Označme ještě 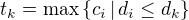 . Definujme potom
. Definujme potom 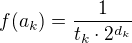 , v ostatních bodech libovolně (dodefinujeme spojitě tak, aby byla rostoucí). Pak pro
, v ostatních bodech libovolně (dodefinujeme spojitě tak, aby byla rostoucí). Pak pro  platí
platí  , jelikož
, jelikož  a tím pádem i
a tím pádem i 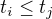 . Řada
. Řada 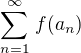 pak konverguje, protože její částečný součet nikdy nepřesáhne jedničku.
pak konverguje, protože její částečný součet nikdy nepřesáhne jedničku.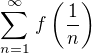 konverguje. Sestrojme posloupnost následovně: půjde opět o seřazená čísla tvaru
konverguje. Sestrojme posloupnost následovně: půjde opět o seřazená čísla tvaru  , jen se bude každé vyskytovat vícekrát za sebou - právě
, jen se bude každé vyskytovat vícekrát za sebou - právě 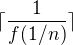 -krát. Řada, která vznikne, když tuto posloupnost "proženeme" funkcí
-krát. Řada, která vznikne, když tuto posloupnost "proženeme" funkcí 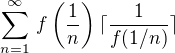 .
. patří do definičního oboru funkce
patří do definičního oboru funkce 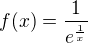 ?
?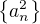 nesmí být monotónní, jinak by řada třetích mocnin konvergovala podle Dirichletova kritéria. Dále musí být
nesmí být monotónní, jinak by řada třetích mocnin konvergovala podle Dirichletova kritéria. Dále musí být 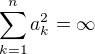 , jinak by třetí mocniny konvergovaly podle Abelova kritéria (možná mám ta kritéria naopak).
, jinak by třetí mocniny konvergovaly podle Abelova kritéria (možná mám ta kritéria naopak).