Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Lichoběžník (MO - 60. r. - Z9-III-2) (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 03. 2011 15:08
Lichoběžník (MO - 60. r. - Z9-III-2)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 23. 03. 2011 21:03 — Editoval BakyX (23. 03. 2011 21:17)
Re: Lichoběžník (MO - 60. r. - Z9-III-2)
↑ byk7:
Ahoj..Úplne rovnako ako tebe. Mohol by som mať 24 bodov.
Túto úlohu som už na tomto fóre riešil..Presne rovnakú..Ak chceš, nájdi ju ;)
EDIT: http://forum.matweb.cz/viewtopic.php?id=24735
1^6 - 2^6 + 3^6 = 666
Offline
#6 23. 03. 2011 21:25
Re: Lichoběžník (MO - 60. r. - Z9-III-2)
↑ byk7:
To ma napadlo, využiť podobnosť trojuholníkov. Ale nakoniec som to riešil úplne inak a to by bolo nadlhšie. Vyjadril som výšky tých trojuholníkov a zostavil rovnice a tak.
1^6 - 2^6 + 3^6 = 666
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Lichoběžník (MO - 60. r. - Z9-III-2) (TOTO TÉMA JE VYŘEŠENÉ)


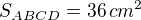 .
. kde
kde  je koeficient podobnosti trojúhelníků ABM, CMD (
je koeficient podobnosti trojúhelníků ABM, CMD (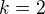 ).
).