Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » izometria na kompakte (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 01. 2012 17:15
izometria na kompakte
ahojte chcel by som poprosiť o návod (naozaj len návod)
na dôkaz tvrdenia,že ak 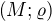 je kompaktný metrický priestor(z každej postupnosti sa dá vybrať konvergentná podpostupnosť) a
je kompaktný metrický priestor(z každej postupnosti sa dá vybrať konvergentná podpostupnosť) a 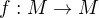 je izometria(zachováva vzdialenosti) tak
je izometria(zachováva vzdialenosti) tak 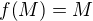
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#3 29. 01. 2012 18:20
Re: izometria na kompakte
↑ Olin:díky čiže keby bola  neprázdna tak by bola okolo ľubovoľného jej bodu guľa , ktorá je celá v nej a obraz tej gule by bol vďaka izometrii opäť tá istá guľa teda je tam spor,lebo tá guľa je podmnožinou doplnku obrazu teda je
neprázdna tak by bola okolo ľubovoľného jej bodu guľa , ktorá je celá v nej a obraz tej gule by bol vďaka izometrii opäť tá istá guľa teda je tam spor,lebo tá guľa je podmnožinou doplnku obrazu teda je 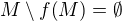 je to tak?
je to tak?
MATH IS THE BEST!!!
Offline
#7 30. 01. 2012 14:30
Re: izometria na kompakte
Dnes dopoledne jsem si uvědomil, že mé původní řešení je špatně, takže bych tu mou "nápovědu" bral s rezervou. Vymyslel jsem ale jedno snad už funkční, tak opět nějaký pokus o návod:
Offline
#8 30. 01. 2012 14:58
Re: izometria na kompakte
↑ Olin:
Ahoj.
Ta maximální  -síť
-síť  (maximální v tom smyslu, že žádná její nadmnožina už není
(maximální v tom smyslu, že žádná její nadmnožina už není  -sítí) by se jistě dala nějak sestrojit, ale maximálních
-sítí) by se jistě dala nějak sestrojit, ale maximálních  -sítí k danému
-sítí k danému 
může existovat nekonečně mnoho. Když vedle  i
i  je maximální
je maximální  -síť , plyne z toho něco ?
-síť , plyne z toho něco ?
Offline
#9 30. 01. 2012 15:54 — Editoval jarrro (30. 01. 2012 15:55)
Re: izometria na kompakte
↑ Rumburak:a čo s tou postupnosťou?rozmýšlal som, ale nie je konštantná?
MATH IS THE BEST!!!
Offline
#11 30. 01. 2012 16:27 — Editoval Rumburak (30. 01. 2012 16:38)
Re: izometria na kompakte
↑ jarrro:
Označme  střed koule
střed koule 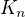 , takže
, takže 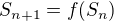 , jak plyne z definice těchto koulí a faktu, že
, jak plyne z definice těchto koulí a faktu, že  je isometrie.
je isometrie.
I. Nechť nejprve 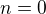 . Z definice koule
. Z definice koule 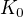 plyne, že
plyne, že 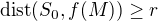 .
.
II. Když  , potom
, potom  , proto a podle I. je
, proto a podle I. je 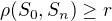 ,
,
odtud a z opětovného použití faktu, že  je isometrie, indukcí dostáváme
je isometrie, indukcí dostáváme  .
.
Z posloupnosti  proto nelze vybrat takovou, která by splňovala BC podmínku, a tedy ani takovou,
proto nelze vybrat takovou, která by splňovala BC podmínku, a tedy ani takovou,
která by byla konvergentní. To je ale ve sporu s předpokladem o kompaktnosti prostoru 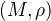 .
.
Offline
#13 30. 01. 2012 18:26 — Editoval jarrro (30. 01. 2012 18:30)
Re: izometria na kompakte
↑ Rumburak:ďakujem toto by ma nenapadlo aj pre toto mám rád matematiku, že väčšina dôkazov je zrozumiteľná,ale vyžaduje nápad.
inak napadlo ma,že som riadny drúk toto by chcelo tému najväčšie hlúposti veď tá guľa je mimo obraz a ja zapílim,že sa zobrazí do seba
MATH IS THE BEST!!!
Offline
#14 30. 01. 2012 18:54
Re: izometria na kompakte
Zajímavé, že v obou důkazech se v podstatě dokázalo následující:
Je-li  totálně omezený metrický prostor a
totálně omezený metrický prostor a  isometrie, pak
isometrie, pak 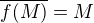 .
.
Zajímal by mě příklad takového totálně omezeného prostoru  a isometrie
a isometrie  , že by platilo
, že by platilo 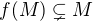 (pokud vůbec existuje).
(pokud vůbec existuje).
Offline
#16 31. 01. 2012 09:30
Re: izometria na kompakte
↑ Olin:
Díky, tento závěrečný krok už chápu. Celý ten důkaz je, myslím, postaven na větě
V. Ke každému  existuje přirozené číslo
existuje přirozené číslo 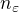 takové, že
takové, že
(1) v  existuje
existuje  -síť mohutnosti
-síť mohutnosti 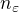 ,
,
(2) v  neexistuje
neexistuje  -síť mohutnosti větší než
-síť mohutnosti větší než 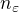 .
.
Tuto větu potřebujeme k tomu, aby  byla maximální sítí nejen v
byla maximální sítí nejen v 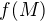 , což je triviální, ale také v
, což je triviální, ale také v  . Avšak jak je to s její platností,
. Avšak jak je to s její platností,
pokud jde o její tvrzení (2) , mi ještě není jasné. Samozřejmě rozumím tomu, že pro žádné  neexistuje
neexistuje  -síť nekonečné mohutnosti,
-síť nekonečné mohutnosti,
což je ekvivalentní totální omeznosti toho prostoru. Ale věta V mi připadá ještě o něco silnější a dokázat ji se mi zatím nedaří.
Offline
#17 31. 01. 2012 10:57 — Editoval Olin (31. 01. 2012 11:07)
Re: izometria na kompakte
↑ Rumburak:
Myslím, že by to mělo jít takto:
Vezměme nějakou maximální  -síť
-síť  a libovolnou
a libovolnou  -síť
-síť  . Z maximality
. Z maximality  je jasné, že
je jasné, že  , což znamená, že systém
, což znamená, že systém  je pokrytí
je pokrytí  (otevřenými) koulemi o poloměru
(otevřenými) koulemi o poloměru  . Z trojúhelníkové nerovnosti se snadno nahlédne, že pro
. Z trojúhelníkové nerovnosti se snadno nahlédne, že pro  ,
,  platí
platí 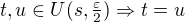 , odkud plyne
, odkud plyne 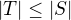 , neboli každá
, neboli každá  -síť má nejvýše
-síť má nejvýše  prvků.
prvků.
K existenci maximálních
 -sítí: ta plyne z toho, že v (částečném) uspořádání
-sítí: ta plyne z toho, že v (částečném) uspořádání  -sítí inklusí je díky totální omezenosti každý řetězec pouze konečný. Eventuelně lze použít princip maximality, ale to je v tomto případě kanon na vrabce.
-sítí inklusí je díky totální omezenosti každý řetězec pouze konečný. Eventuelně lze použít princip maximality, ale to je v tomto případě kanon na vrabce. Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » izometria na kompakte (TOTO TÉMA JE VYŘEŠENÉ)

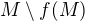 je otevřená množina.
je otevřená množina. o poloměru
o poloměru  a zkoumal bych množinovou posloupnost
a zkoumal bych množinovou posloupnost  ,
,  .
.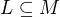 nazveme
nazveme  mají vzdálenost aspoň
mají vzdálenost aspoň  je
je  , což s uzavřeností
, což s uzavřeností 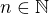
 (ve které máme dokonce očíslované prvky), vybereme konvergentní podposloupnost prvních prvků, druhých prvků, … (diagonální metoda výběru). Výsledná nekonečná množina je "skoro"
(ve které máme dokonce očíslované prvky), vybereme konvergentní podposloupnost prvních prvků, druhých prvků, … (diagonální metoda výběru). Výsledná nekonečná množina je "skoro"