Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Aplikace určitého integrálu - objem tělesa (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 02. 2012 19:21
Aplikace určitého integrálu - objem tělesa
Dobrý den, chtěl bych se zeptat, jak na postup v tomto zadání? Mělo by to vyjít (3/2)*pi
Zadání:
Vypočítejte objem tělesa, které vznikne rotací plochy mezi křivkami y = x^2 +1, y = 0, x = 1
a x = 0 kolem osy y.
Zde moje úvaha:![kopírovat do textarea $V=\pi \int_{0}^{1} (y-1)*dy=[\frac{y^{2}}{2}-y]^{1}_{0} =\frac{1}{2}\pi $](/mathtex/8d/8d2e65e6f9aa4ea1b2a69ab48d3926f3.gif)
Předem děkuji za odpověď
Offline
- (téma jako vyřešené označil(a) Neony)
#2 03. 02. 2012 21:17 — Editoval Rumburak (07. 02. 2012 10:09)
Re: Aplikace určitého integrálu - objem tělesa
↑ Neony:
Úvaha správná, Jsou tam ale drobné chyby. Pro x=1 vyjde y = 2, takže![kopírovat do textarea $V=\pi \int_{0}^{2} x^2(y)\,\mathrm{d}y=\pi \int_{0}^{2} (y-1)\,\mathrm{d}y=\pi \left[\frac{y^{2}}{2}-y\right]^{2}_{0} =\frac{3}{2}\pi $](/mathtex/7e/7e341cb4fd1ad85a89374795e2d0b972.gif) .
.
EDIT. Tento příspěvek beru zpět, viz ↑ Rumburak:
Offline
#5 06. 02. 2012 10:00 — Editoval Rumburak (06. 02. 2012 10:30)
Re: Aplikace určitého integrálu - objem tělesa
↑ Neony:
Ahoj, s časovým odstupem teď vidím a musím sebekriticky a s omluvou přiznat, že můj postup v ↑ Rumburak: byl bohužel chybný .
Základem našeho tělesa je rotační válec výšky 2, jehož dolní podstavou je kruh  . Shora je toto těleso ohraničeno
. Shora je toto těleso ohraničeno
čásí plochy vzniklé rotací paraboly  okolo osy y. Ze základního válce je tak shora vyříznuta úseč rotačního paraboloidu,
okolo osy y. Ze základního válce je tak shora vyříznuta úseč rotačního paraboloidu,
jejíž objem musíme odečíst od objemu  základního válce. Objem tělesa, které nás zajímá, proto bude
základního válce. Objem tělesa, které nás zajímá, proto bude ![kopírovat do textarea $V=2\pi - \pi \int_{1}^{2} x^2(y)\,\mathrm{d}y=2\pi - \pi\int_{1}^{2} (y-1)\,\mathrm{d}y=2\pi - \pi \left[\frac{y^{2}}{2}-y\right]^{2}_{1}=2\pi - \frac{1}{2}\pi =\frac{3}{2}\pi$](/mathtex/e9/e956ed84a47a19e97d4a0a0df5f31df7.gif) .
.
Výpočet by šlo provést též jinými metodami, například pomocí dvojného či trojného integrálu , nebo podle vzorce, který doporučil kolega Honzc.
Administrátory pak prosím o odebrání bodu nezaslouženě mi uděleného za předchozí chybný příspěvek.
Offline
#6 06. 02. 2012 20:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aplikace určitého integrálu - objem tělesa
↑ Rumburak:
Kolegovi Neony jsem poslala upozorňující mail ohledně opravy a, kdyby nám nezamrznul inkoust, tak bych Tebe připsala na nástěnku.
To z mého pohledu je dostačuji (těžce udřené Admiratorstvo bych už nerušila). Zdravím :-)
-------------------------------- že naše Johanna píše krásně a přesně:
"...Tak toužebně vzdychám po únoru, jenž mne konečně spasí a navrátí milému druhu a příteli, psacímu stolu! Co jsem mohla zde napsati, kdyby nebylo těch neustálých dopisů do pisárny bývalo! Věř mi, že hodně dlouhou novelu. Musela jsem si se věru sama sobě několikrát pousmáti, že zdraví svého šetřím nedopřejíc si příjemné práce, a nepříjemné že každý den alespoň dvě hodiny hlavu, oči a rozmar obětuji."
Offline
#8 07. 02. 2012 10:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aplikace určitého integrálu - objem tělesa
↑ Rumburak:
no výborně, alespoň máme co číst v novinkách :-)
Ano, z "Literárního soukromí" z období, kdy byla nucena se aktivně a veřejně angažovat za údajné osvobození žen. Ještě zjisti, prosím, z díla kterého ruského autora je únor a inkoust (je přeloženo do češtiny, tedy nebude problém) a budeme považovat téma za zcela vyřešené.
Zdravím :-)
Offline
#9 07. 02. 2012 11:35
Re: Aplikace určitého integrálu - objem tělesa
↑ jelena:
Bude to problém :-), protože významných ruských spisovatelů a jejich děl bylo mnoho, zatímco já jsem četl jen něco málo
(od L.N.Tolstého, Puškina, Jefremova, Solženicyna, Pasternaka, Katejeva a Gajdara).
Offline
#10 07. 02. 2012 11:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aplikace určitého integrálu - objem tělesa
↑ Rumburak:
tak z toho mala (což je celkem pěkný seznam) určitě už vybereš - je tam :-)
Offline
#11 11. 02. 2012 12:37 — Editoval Neony (11. 02. 2012 12:37)
Re: Aplikace určitého integrálu - objem tělesa
↑ Rumburak:
Pěkný den, chybovat je lidské a :) s tím se musí počítat (já už si toho též nevšiml - nepřepočítával jsem to)... Jinak děkuji velice za opravu a tak si plusový bod určitě zasloužíte!!
Offline
#13 14. 02. 2012 13:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aplikace určitého integrálu - objem tělesa
↑ Neony:
Také děkuji.
↑ Rumburak:
pro pořádek: Je to Pasternak - "Únor" (nepříliš správná báseň na můj pohled, neb se těší na duben, ovšem "Zimní noc" je správná báseň, neb všude byla vánice - v únoru). Obě jsou do češtiny přeloženy, originály zde například. Hezké čtení přeji a zdravím.
Offline
#14 14. 02. 2012 13:49
Re: Aplikace určitého integrálu - objem tělesa
↑ jelena:
Díky za informaci. Během svého dvoutýdenního pobytu v Moskvě (už je to řada let) jsem vyhledal Pasternakův hrob v nedalekém Peredelkinu.
Avšak četl jsem od něho pouze slavného Dr. Živága - ke čtení poesie se odhodlávám pouze výjimečně - asi nemám pro ni ty správné buňky.
Zdravím též :-) .
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Aplikace určitého integrálu - objem tělesa (TOTO TÉMA JE VYŘEŠENÉ)

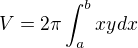
![kopírovat do textarea $V=2\pi \int_{0}^{1}x(x^{2}+1)dx=2\pi[\frac{x^{4}}{4}+\frac{x^{2}}{2}]^{1}_{0}=2\pi\frac{3}{4}=\frac{3}{2}\pi $](/mathtex/cd/cdf9805624dbde33cbb022d63e24013b.gif)