Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Dôkaz rovnosti - veľmi pekná úloha (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 08. 2011 23:20 — Editoval BakyX (25. 06. 2012 14:59)
Dôkaz rovnosti - veľmi pekná úloha
Zdravím..Iste uznáte, že táto úloha je jednoducho pekná :)
Dokážte, že ak pre čísla  platí:
platí: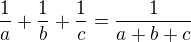 , tak pre ľubovoľné nepárne
, tak pre ľubovoľné nepárne 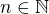 platí:
platí: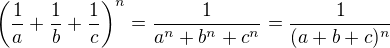
1^6 - 2^6 + 3^6 = 666
Offline
- (téma jako vyřešené označil(a) BakyX)
#2 23. 08. 2011 19:52 Příspěvek uživatele byk7 byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#3 23. 08. 2011 20:56 Příspěvek uživatele Stýv byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#4 23. 08. 2011 21:11 — Editoval OiBobik (23. 08. 2011 21:19) Příspěvek uživatele OiBobik byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#5 23. 08. 2011 21:16 Příspěvek uživatele BakyX byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#6 23. 08. 2011 21:54 Příspěvek uživatele Stýv byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#7 23. 08. 2011 22:00 — Editoval musixx (23. 08. 2011 22:03) Příspěvek uživatele musixx byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#8 24. 08. 2011 16:51 Příspěvek uživatele byk7 byl skryt uživatelem byk7. Důvod: na žádost BakyXe
#10 27. 06. 2012 22:51
- check_drummer

- Příspěvky: 4628
- Reputace: 99
Re: Dôkaz rovnosti - veľmi pekná úloha
↑ BakyX:
Ahoj, jeden postřeh, který není asi ani třeba skrývat:
Rovnost 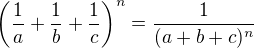 je zřejmá - dokonce i pro sudá n, tedy stačí dokázat
je zřejmá - dokonce i pro sudá n, tedy stačí dokázat  , což vypadá jako nějaký pěkný homomorfismus...
, což vypadá jako nějaký pěkný homomorfismus...
"Máte úhel beta." "No to nemám."
Offline
#11 27. 06. 2012 23:13 Příspěvek uživatele byk7 byl skryt uživatelem byk7. Důvod: OT
#12 28. 06. 2012 16:29
- check_drummer

- Příspěvky: 4628
- Reputace: 99
Re: Dôkaz rovnosti - veľmi pekná úloha
Nyní již skrývám:
"Máte úhel beta." "No to nemám."
Offline
#13 28. 06. 2012 20:32
Re: Dôkaz rovnosti - veľmi pekná úloha
1^6 - 2^6 + 3^6 = 666
Offline
#14 28. 06. 2012 21:19
- check_drummer

- Příspěvky: 4628
- Reputace: 99
Re: Dôkaz rovnosti - veľmi pekná úloha
"Máte úhel beta." "No to nemám."
Offline
#15 29. 06. 2012 15:39
Re: Dôkaz rovnosti - veľmi pekná úloha
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 01. 07. 2012 15:12
- check_drummer

- Příspěvky: 4628
- Reputace: 99
Re: Dôkaz rovnosti - veľmi pekná úloha
↑ vanok:
Ahoj - právě proto jsem psal do závorek, že n je liché (po slovensky "nepárné"). :-)
"Máte úhel beta." "No to nemám."
Offline
#17 01. 07. 2012 18:14
Re: Dôkaz rovnosti - veľmi pekná úloha
↑ check_drummer:
dakujem
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Dôkaz rovnosti - veľmi pekná úloha (TOTO TÉMA JE VYŘEŠENÉ)

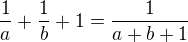 chápané po úpravě jako kvadratickou rovnici s neznámou a zjistíme, že a=-1 nebo a=-b, což po dosazení do
chápané po úpravě jako kvadratickou rovnici s neznámou a zjistíme, že a=-1 nebo a=-b, což po dosazení do 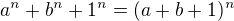 (n liché) dá platnou identitu 1=1. Opačným postupm (úpravy jsou ekvivaletní) získáme
(n liché) dá platnou identitu 1=1. Opačným postupm (úpravy jsou ekvivaletní) získáme 
 dana rovnost ma riesenia tejto formy: dve cisla z
dana rovnost ma riesenia tejto formy: dve cisla z  su opacneho znamienka a maju tu istu absolutnu hodnotu a tretie cislo je lubovolne nenulove cislo.
su opacneho znamienka a maju tu istu absolutnu hodnotu a tretie cislo je lubovolne nenulove cislo.