Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 09. 2012 10:39 — Editoval Pavel Brožek (29. 09. 2012 10:50)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Tvar planety
Planeta má hmotnost M a moment hybnosti L, hustotu má všude stejnou  . Jaký je její ideální tvar?
. Jaký je její ideální tvar?
Offline
#2 30. 09. 2012 18:29
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Ahoj, co znamená ideální tvar? Minimalizující nějakou veličinu (jakou)? Díky za info.
"Máte úhel beta." "No to nemám."
Offline
#3 30. 09. 2012 18:31 — Editoval Pavel Brožek (02. 10. 2012 20:27)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Myslel jsem tím minimalizující energii, což by mělo být asi to samé, jako kdybychom uvažovali, že to bude planeta složená z tekutiny a zajímali bychom se o tvar po ustálení.
Offline
#4 30. 09. 2012 19:38
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Jen se zeptám - využíváš k řešení variačního počtu?
"Máte úhel beta." "No to nemám."
Offline
#5 30. 09. 2012 19:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Popravdě, já řešení vzdal, je to asi moc komplikované :-)
Offline
#6 30. 09. 2012 20:24
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Také v tuto chvíli nevím jak na to, fyzika není můj šálek kávy. (Tak se pokusme nějakou diskusí dojít alespoň ke konstrukci vyjádření té energie pro libovolný tvar planety, třeba jako nějaký integrál.)
Možná se díky výše uvedenému zeptám dost naivně: Moment hybnosti závisí, stručně řečeno, na vzdálenosti od osy rotace a na rychlosti rotace. Energií máš na mysli kinetickou energii (závisející na rychlosti otáčení a hmotnosti daného hmotného bodu)?
Jinak ze zadání dle mého plyne, že planeta má konstantní (pevně daný) objem a tedy díky symetrii lze dle mého uvažovat nějaký libovolný řez vedený osou planety a jeho "obrysovou křivku" f a pro body mezi touto křivkou a osou rotace nějakým integrálním součtem vyjádřit podmínku na konstantní hybnost a jiným integrálním součtem hodnotu energie. Kdyžtak mě zadrž, pokud je to zcestné. Ale pokud není, tak jsi na toto určitě už přišel.
Jen ještě přemýšlím o tom, že u té planety vlastně vůbec neuvažujeme to, že jsou spolu její části nějak silově vázány (např. gravitačně nebo jinak), tak vůbec dle mého není zřejmé a dle mého to tak ani nemusí být, že uvedená funkce f (kontura planety) výše bude spojitá... Nebo spojitost z něčeho plyne?
"Máte úhel beta." "No to nemám."
Offline
#7 30. 09. 2012 22:18 — Editoval Pavel Brožek (30. 09. 2012 22:20)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Uvažujeme samozřejmě gravitační sílu (klasicky Newtonovskou), která právě ten tvar planety vytvoří. Další síly neuvažujeme. Samozřejmě tam jiné síly jsou (aby se planeta gravitačně nezhroutila), ale ty jsou pro nás pohodlně popsány požadavkem konstantní hustoty v celém objemu planety, takže je dál neuvažujeme. Ve výrazu pro energii je zanedbáme (kdybychom nezanedbali, tak tam bude např. nějaké povrchové napětí, které se bude snažit zmenšit povrch planety).
Zavedeme si cylindrické souřadnice  . Toto zavedení
. Toto zavedení  mi umožní psát hezky integrály pro určení kinetické energie a momentu hybnosti.
mi umožní psát hezky integrály pro určení kinetické energie a momentu hybnosti.
Pro gravitační potenciál v místě  platí
platí
kde  je planeta. Celková potenciální energie tedy je
je planeta. Celková potenciální energie tedy je
Celková kinetická energie: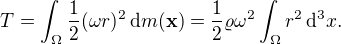
Celková energie:
Celkový moment hybnosti:
Celková hmotnost:
Volnost je tedy v  a
a  (
( můžeme případně vyloučit dosazením z (2) do (1)). Musíme tedy najít tvar planety
můžeme případně vyloučit dosazením z (2) do (1)). Musíme tedy najít tvar planety  a úhlovou rychlost
a úhlovou rychlost  takové, že je minimalizována energie (1) při splnění rovností (2) a (3).
takové, že je minimalizována energie (1) při splnění rovností (2) a (3).
Teď už je to jen matematický problém. Předpokládal bych, že tvar bude „hezký“, tj. žádné nespojitosti a podobně.
Offline
#8 01. 10. 2012 00:14 — Editoval check_drummer (01. 10. 2012 00:16)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Ahoj, nebylo by možné dosadit (2) do (1) za T získat tak člen  ? (Edit: Teď jsem si všiml, že to máš asi také na mysli v textu výše.)
? (Edit: Teď jsem si všiml, že to máš asi také na mysli v textu výše.)
Nebylo by možné na základě úvah o symetrii uvažovat tvar  že je rotačně symetrický a na základě úvah o minimu energie i to, že je bez děr, že řez rovinou procházející osou rotace opravdu tvoří nějakou "hranici" (povrch planety) nezávislou na úhlu řezu? A i kdyby to nebylo zřejmé, nebylo by vhodnější pro začátek předpokládat, že toto lze?
že je rotačně symetrický a na základě úvah o minimu energie i to, že je bez děr, že řez rovinou procházející osou rotace opravdu tvoří nějakou "hranici" (povrch planety) nezávislou na úhlu řezu? A i kdyby to nebylo zřejmé, nebylo by vhodnější pro začátek předpokládat, že toto lze?
Víš jaký má být výsledek? Odkud úloha pochází?
"Máte úhel beta." "No to nemám."
Offline
#9 01. 10. 2012 00:25 — Editoval Pavel Brožek (01. 10. 2012 00:29)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Měl jsem na mysli dosadit z (2) do (1) za  . Tím bychom se zbavili volného parametru
. Tím bychom se zbavili volného parametru  . Pokud dosadíme z (2) do (1) jak píšeš ty, stále musíme splnit rovnici (2), nemůžeme ji po takovém dosazení považovat za splněnou a dál ji neuvažovat. Ale možná je to tvar, s kterým se pak bude lépe pracovat.
. Pokud dosadíme z (2) do (1) jak píšeš ty, stále musíme splnit rovnici (2), nemůžeme ji po takovém dosazení považovat za splněnou a dál ji neuvažovat. Ale možná je to tvar, s kterým se pak bude lépe pracovat.
Ano, považoval bych tvar za rotačně symetrický, bez děr a popisoval bych ho rovnicí povrchu  s neznámou funkcí f, kterou budeme hledat.
s neznámou funkcí f, kterou budeme hledat.
Nevím, jaký má být výsledek a ani jestli je reálné se k něčemu rozumnému dobrat. Na netu jsem viděl nějaká řešení pro mírně eliptický tvar (gravitační síla se pak bere přibližně jako centrální), kde se snad odvodí vztah mezi excentricitou a úhlovou rychlostí.
Úloha (lépe řečeno inspirace) pochází z tohoto tématu :-)
Offline
#10 02. 10. 2012 17:02
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Ahoj,
předložím svůj názor, jistě mi budeš oponovat:
Minimalizujeme tedy součet U+T. Jak jsme psal výše, T přejde na  .
.
U je tvaru 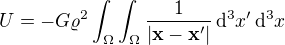 .
.
Dle mého U nezávisí na  , takže když zvolím
, takže když zvolím  , pak bude T nejmenší možné (0) a na U to vliv nemá.
, pak bude T nejmenší možné (0) a na U to vliv nemá.
U nezávisí na ničem jiném než na vzájemné poloze (resp. vzdálenosti) bodů planety a dle mého by mělo být možné ukázat, že uvedený integrál - a sice  je minimální pro kouli.
je minimální pro kouli.
Takže mi z toho vychází, že planeta je koule, která nerotuje... Na druhou stranu, pak by vyšla celková energie záporná, což nevím zda může nastat...
"Máte úhel beta." "No to nemám."
Offline
#11 02. 10. 2012 19:14 — Editoval Pavel Brožek (02. 10. 2012 19:16)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Ahoj, s tím, že celková energie je záporná problém není – to souvisí s tím, jak volíme nulovou hladinu potenciální energie. Pro dvě tělesa ji volíme tak, že pokud jsou tělesa „nekonečně vzdálená“, pak je nulová, takže když se k sobě budou přibližovat, musí potenciální energie klesat do záporných hodnot, aby síla byla přitažlivá (síla je úměrná záporně vzaté derivaci potenciální energie). Takové volbě odpovídají intergrály, které jsem napsal.
Pokud zvolíš  tak nebude splněna rovnice (2), takže je to špatná volba. To je přesně to, o čem jsem psal v minulém příspěvku. Tím, že dosadíš z (2) do (1) tím tvým způsobem, nezaručuje, že už můžeme (2) zahodit.
tak nebude splněna rovnice (2), takže je to špatná volba. To je přesně to, o čem jsem psal v minulém příspěvku. Tím, že dosadíš z (2) do (1) tím tvým způsobem, nezaručuje, že už můžeme (2) zahodit.
Offline
#12 02. 10. 2012 19:36
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
To je pravda a dává to i smysl: Hodnoty U a L jdou opravdu proti sobě: Chceme-li, aby v U+T  byla co nejmenší (to je to moje dosazení, kdy T závisí jen na
byla co nejmenší (to je to moje dosazení, kdy T závisí jen na  ), pak díky (2) by měly být body planety co nejdále od osy rotace. Na druhou stranu tímto by pak U mělo příliš (v absolutní hodnotě) malou zápornou hodnotu, protože by se příliš odchylovalo od "gravitačně ideální" koule. Tedy tvar bude opravdu nejspíš nějaký "rozumný" mezi koulí a plochým diskem (nebo (dutým) válcem?) kolmým k ose rotace.
), pak díky (2) by měly být body planety co nejdále od osy rotace. Na druhou stranu tímto by pak U mělo příliš (v absolutní hodnotě) malou zápornou hodnotu, protože by se příliš odchylovalo od "gravitačně ideální" koule. Tedy tvar bude opravdu nejspíš nějaký "rozumný" mezi koulí a plochým diskem (nebo (dutým) válcem?) kolmým k ose rotace.
Zkusím se zamyslet nad tím nahrazením  pomocí kontury f a tím (jednoduše řečeno) zkusit převést
pomocí kontury f a tím (jednoduše řečeno) zkusit převést  na
na 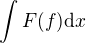 ...
...
"Máte úhel beta." "No to nemám."
Offline
#13 02. 10. 2012 19:59 — Editoval Pavel Brožek (02. 10. 2012 21:05)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Možná bych pro jednoduchost zkusil začít tím, že budeme předpokládat tvar elipsoidu  . Potom snadno dostaneme
. Potom snadno dostaneme
Po vyloučení  dostáváme funkci
dostáváme funkci
kterou minimalizujeme na množině 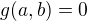 pro
pro
Teď už zbývá jen spočítat ten integrál v 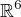 :-)
:-)
Offline
#14 02. 10. 2012 20:43
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Jestli to tedy dobře chápu, úkolem je najít a,b? Z čeho plyne podmínka g(a,b)=0?
"Máte úhel beta." "No to nemám."
Offline
#15 02. 10. 2012 21:04 — Editoval Pavel Brožek (02. 10. 2012 21:06)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
Ano, úkolem je najít a a b, tedy délku poloos elipsoidu. Tím už bude tvar elipsoidu jeznoznačně určen.
Ta podmínka 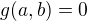 plyne z toho, že hmotnost M je zadaná (minimalizujeme energii při daném M a L). Když si hmotnost vyjádříme pomocí a,b, dostaneme
plyne z toho, že hmotnost M je zadaná (minimalizujeme energii při daném M a L). Když si hmotnost vyjádříme pomocí a,b, dostaneme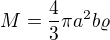 .
.
Edit: Teď jsem si všimnul, že mi v předchozím příspěvku ve vyjádření funkce  vypadlo
vypadlo  , proto ses ptal? Opravil jsem to.
, proto ses ptal? Opravil jsem to.
Offline
#16 02. 10. 2012 21:58 — Editoval check_drummer (02. 10. 2012 22:03)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Bylo mi divné, odkud se ten výraz vzal, když se jinde nevyskytoval. :-)
A vidím, že L jsi již do minimalizované funkce dosadil - jinými slovy podmínku na konstantnost L nemusíme řešit, protože tu zajistíme nakonec vhodnou volbou  , že?
, že?
Edit: Teď vidím, že to nemá smysl, protože tak bychom pro všechny tvary elipsoidu získali stejnou hodnotu toho integrálu...
"Máte úhel beta." "No to nemám."
Offline
#17 02. 10. 2012 23:15 — Editoval Pavel Brožek (02. 10. 2012 23:15)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
Narazil jsem na tento článek: On the gravitational energy of ellipsoidal bodies and some related functions.
Pokud jsem tam tomu dobře porozuměl a vše správně upravil, tak by výsledek měl být (po dosazení za b)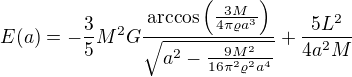
Vzal jsem hodnoty pro Zemi (z wikipedie, moment hybnosti jsem nenašel, tak jsem ho dopočítal jako pro homogenní kouli) a dostal jsem
což zhruba odpovídá hodnotám uváděným na wikipedii
Tipuji, že rozdíl bude způsobený hlavně tím, že jsem považoval hustotu za konstantní.
Offline
#18 02. 10. 2012 23:30
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Tvar planety
↑ check_drummer:
L považujeme za konstantní a dané, takže jakmile určíme a a b, tak  dopočítáme z
dopočítáme z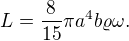
Není to tak, že bychom si  mohli zvolit. To dostaneme jako výsledek minimalizace energie.
mohli zvolit. To dostaneme jako výsledek minimalizace energie.
Offline
#19 04. 10. 2012 09:51 — Editoval pietro (04. 10. 2012 10:02)
Re: Tvar planety
Zdravím Vás vzácni páni !
↑ Pavel Brožek:↑ check_drummer:
zaujali ma Vaše postupy a ďakujem za poskytnuté riešenia.
Nemôžem si pomôcť , ale aj tu http://cs.wikipedia.org/wiki/Zplo%C5%A1t%C4%9Bn%C3%AD
sa vyskytuje pojem elasticita v blízkej súvislosti s našim problémom.
Celkom zaujímavá je gravimetrická mapa ČR
Offline
#20 05. 10. 2012 13:19
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Tvar planety
↑ Pavel Brožek:
Ahoj, špatně jsem se vyjádřil, měl jsem na mysli to, že  je potom již jednoznačně dána.
je potom již jednoznačně dána.
"Máte úhel beta." "No to nemám."
Offline
 na množině bodů, pro které je funkce
na množině bodů, pro které je funkce  nulová, tedy na kružnici o poloměru 1. I když na této množině platí
nulová, tedy na kružnici o poloměru 1. I když na této množině platí  , tak pořád nemůžeme podmínku
, tak pořád nemůžeme podmínku 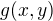 zahodit, jinak bychom mohli říct, že funkce může nabývat libovolně malých hodnot pro
zahodit, jinak bychom mohli říct, že funkce může nabývat libovolně malých hodnot pro  . To bychom ale utekli z množiny, která nás zajímá.
. To bychom ale utekli z množiny, která nás zajímá.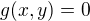 vyjádřím třeba
vyjádřím třeba  , dosadím do
, dosadím do  a budu minimalizovat na množině
a budu minimalizovat na množině ![kopírovat do textarea $x\in[-1,1]$](/mathtex/f7/f7b2009c5a761b979b09452fe39725b5.gif) .
.