Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Hilbertov priestor (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 10. 2012 16:15 — Editoval ajeto (20. 10. 2012 21:40)
Hilbertov priestor
Dobrý deň,
mám vektorový priestor  všetkých spojitých funkcií na intervale
všetkých spojitých funkcií na intervale ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) takých, že platí
takých, že platí
na ktorom je definovaný skalárny súčin predpisom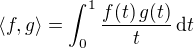 .
.
Otázka znie, či je priestor  so skalárnym súčinom
so skalárnym súčinom  Hilbertov.
Hilbertov.
Predpokladám, že metrika v priestore  odvodená z normy odvodenej zo skalárneho súčinu
odvodená z normy odvodenej zo skalárneho súčinu
vyzerá nejak takto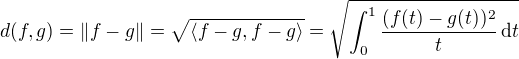
a teraz môžem buď ukázať že každá postupnosť ktorá je fundamentálna v  má v
má v  limitu,
limitu,
alebo nájsť konkrétnu postupnosť funkcií ktorá je v  fundamentálna a jej limitou vzhľadom na
fundamentálna a jej limitou vzhľadom na 
je funkcia ktorá nepatrí do  .
.
Nepodarilo sa mi však ani jedno ani druhé.
Vďaka za každé usmernenie.
Offline
- (téma jako vyřešené označil(a) ajeto)
#2 21. 10. 2012 11:30 — Editoval Pavel Brožek (21. 10. 2012 11:31)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hilbertov priestor
↑ ajeto:
Ahoj, zkusil bych najít posloupnost funkcí z X, které budou konvergovat k 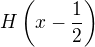 , kde H je Heavisideova funkce.
, kde H je Heavisideova funkce. 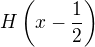 není na intervalu
není na intervalu ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) spojitá, takže nebude z X.
spojitá, takže nebude z X.
Offline
#4 24. 10. 2012 23:58
Re: Hilbertov priestor
↑ Pavel Brožek: ↑ Brano: vďaka za radu,
skúšal som, zatiaľ bez úspechu
Offline
#5 25. 10. 2012 00:06
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hilbertov priestor
↑ ajeto:
Co třeba funkce![kopírovat do textarea $f_n(x)=\begin{cases}
0&\mbox{pro }x\in\[0,\frac12-\frac1n\]\\
\frac12+\frac n2\(x-\frac12\)&\mbox{pro }x\in\(\frac12-\frac1n,\frac12+\frac1n\)\\
1&\mbox{pro }x\in\[\frac12+\frac1n,1\]\\
\end{cases}$](/mathtex/10/1010bb0ba33ccc7f2a18bd6718e67c01.gif)
Offline
#6 25. 10. 2012 00:26
Re: Hilbertov priestor
↑ Pavel Brožek:
skúšal som niečo podobné, ale príliš komplikované
skúsim toto, vďaka.
Offline
#7 10. 11. 2012 21:54 — Editoval ajeto (10. 11. 2012 22:26)
Re: Hilbertov priestor
Dobrý večer
skúšal som aj túto postupnosť funkcií navrhnutú v ↑ Pavel Brožek:,
pri počítaní 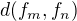 som sa dostal k funkcii tvaru
som sa dostal k funkcii tvaru![kopírovat do textarea $\sqrt{2}\bigg[f_1(m,n)\ln{(g_1(m,n))}+h(m,n)+f_2(m,n)\ln(g_2(m,n))+2m+n\bigg]^{\frac{1}{2}}$](/mathtex/1b/1b6f6bda368ca9cca6b3fccd009eaecb.gif)
kde sa mi zdá byť dosť veľkým problémom práve tá posledná časť 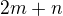 ,
,
z toho zrejme fundamentálnosť postupnosti 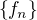 nevytlčiem
nevytlčiem
(tento výraz sa tam s ničím nevykráti pod odmocninou)
je tá postupnosť určite fundamentálna v uvedenej metrike?
vychádzal som z predpokladu  a
a ![kopírovat do textarea $ d(f_m,f_n)=\Bigg[ 2 \Big( \int_{\frac{1}{2}-\frac{1}{n}}^{\frac{1}{2}-\frac{1}{m}} \frac{(f_n(t)-0)^2}{t}\mathrm{d}t +\int_{\frac{1}{2}-\frac{1}{m}}^{\frac{1}{2}} \frac{(f_n(t)-f_m(t))^2}{t}\mathrm{d}t \Big) \Bigg]^{\frac{1}{2}} $](/mathtex/d5/d54d74febe33ee3bf1ddcd41958172a9.gif)
Offline
#8 10. 11. 2012 23:29
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Hilbertov priestor
↑ ajeto:
Já bych to vůbec takhle neintegroval až do konce, ty integrály bych odhadl. V čitateli i jmenovateli máš kladné číslo. Čitatele odhadni maximem, které v obou případech nemůže být větší než 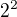 . Jmenovatele odhadni něčím malým, třeba 0,1, to pro dostatečně velká m a n půjde. Integruješ pak už jen konstatní funkci. A velikost těch intervalů, přes které se integruje, půjde do nuly.
. Jmenovatele odhadni něčím malým, třeba 0,1, to pro dostatečně velká m a n půjde. Integruješ pak už jen konstatní funkci. A velikost těch intervalů, přes které se integruje, půjde do nuly.
Snad jsem ten postup naznačil srozumitelně :-)
Offline
#9 11. 11. 2012 04:06
Re: Hilbertov priestor
áno ↑ Pavel Brožek:, zrozumiteľne
škoda že ma táto jednoduchšia cesta nenapadla predtým,
než som sa pokúšal presne spočítať tie integrály :)
vďaka
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Hilbertov priestor (TOTO TÉMA JE VYŘEŠENÉ)