Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyrokova logika - dukaz (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 01. 2013 22:28
Vyrokova logika - dukaz
Ahoj, mam trochu nejasnosti ohledne dukazu ve vyrokove logice. Byl bych moc vdecny za to, kdyby mi to nekdo osvetlil.
Dukaz:
Pro libovolne formule 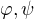 plati
plati 
1) 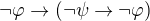 - Instance axiomu A1
- Instance axiomu A1
...
Dukazy jsou mi jasne, tedy az na jednu vec. Obcas se v dukazu objevi podformule u ktere nevim, jak se k ni prislo. V tomto prikladu je to konkretne podformule tvaru 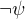 .
.
Instanciovani axiomu A1:  . U podformule
. U podformule  je to jasne, protoze ta je z predpokladu T. Kde se ale vzala negace u
je to jasne, protoze ta je z predpokladu T. Kde se ale vzala negace u 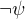 ? Prednasejici to komentoval na prednasce stylem "tady dame negace psi, protoze to muzu, ...", ale uz nezduvodnil proc. Je mi jasne, ze si pravou stranu implikace upravil tak, aby ji mohl pozdeji pouzit pro ucely MP spolu s A3... Ale, ... proc to muzu?
? Prednasejici to komentoval na prednasce stylem "tady dame negace psi, protoze to muzu, ...", ale uz nezduvodnil proc. Je mi jasne, ze si pravou stranu implikace upravil tak, aby ji mohl pozdeji pouzit pro ucely MP spolu s A3... Ale, ... proc to muzu?
-----------------------------------------------------------------------------------------------------------
Pro uplnost, zde jsou definice:
Logicky system 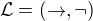
Schema axiomu:
A1: 
A2: 
A3: 
MP: Z  a
a  odvod
odvod 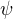
Bud T soubor formuli.
Dukaz formule 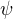 z predpokladu T je konecna posloupnost formuli
z predpokladu T je konecna posloupnost formuli 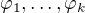 , kde
, kde 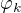 je
je 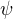 a pro kazde
a pro kazde  , kde
, kde  , plati alespon jedna z nasledujicich podminek:
, plati alespon jedna z nasledujicich podminek:
-  je prvek T;
je prvek T;
-  je instanci jednoho ze schemat A1-A3;
je instanci jednoho ze schemat A1-A3;
-  vznikne aplikaci pravidla MP na formule
vznikne aplikaci pravidla MP na formule 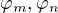 pro vhodne
pro vhodne  .
.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 26. 01. 2013 22:47
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vyrokova logika - dukaz
Pomohlo by, kdybyc první axiom byl 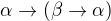
a místo "za psi dáme negaci psi" se řeklo "za alfa dáme negaci phi a za beta dáme negaci psi"? Tady se pouze dosazuje, v tomto kroku neřešíme, co je v předpokladech. Instance axiomu totiž vyplývá z libovolných předpokladů.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyrokova logika - dukaz (TOTO TÉMA JE VYŘEŠENÉ)