Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 02. 2013 21:15
- klarushaaa
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Definiční obor goniometrické funkce
Dobrý večer,
potřebovala bych prosím poradit s příkladem 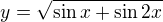 , kde musím spočítat obor hodnot a moc si s tím nevím rady. Předem děkuji za odpověď :)
, kde musím spočítat obor hodnot a moc si s tím nevím rady. Předem děkuji za odpověď :)
Offline
#2 10. 02. 2013 21:23
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Definiční obor goniometrické funkce
↑ klarushaaa: Jediná podmienka je, že výraz pod odmocninou musí byť nezáporný.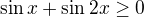

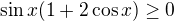
Offline
#3 10. 02. 2013 21:38 — Editoval Freedy (10. 02. 2013 21:42)
Re: Definiční obor goniometrické funkce
BlackFlower. :) jen malá připomínka, chtěl vědět obor HODNOT a né definiční obor.
:D narozdil, v nazvu tematu je Definiční obor :D takže fakt netuším co doopravdy chce
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 10. 02. 2013 21:47 — Editoval Blackflower (10. 02. 2013 21:47)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Definiční obor goniometrické funkce
↑ Freedy: Ďakujem za opravu. Nad oborom hodnôt sa zamyslím a doplním.
Offline
#5 10. 02. 2013 21:55
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Definiční obor goniometrické funkce
Je jasné, že hodnoty funkcie budú nezáporné, čiže potrebujeme ešte zistiť najväčšiu hodnotu, akú môže výraz nadobúdať. To by som riešila asi derivovaním.
Offline
