Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 02. 2014 21:05 — Editoval liamlim (21. 02. 2014 23:04)
nerovnosti
Dobrý den všem!
Před ústředním kolem MO jsem se dnes trochu díval na nerovnosti, protože se mi oproti geometrii toto téma opravdu hodně líbí. Zkoušel jsem využívat Jensenovu nerovnost pomocí které jsem odvodil další nerovnosti. Tyto dvě nerovnosti zde napíšu. A protože si nejsem jistý, jestli jsem po cestě neudělal chybu, bude zadání následující:
Dokažte následující nerovnosti pro kladná  ,
,  ,
,  , nebo nalezněte alespoň jednu trojici kdy nerovnost neplatí
, nebo nalezněte alespoň jednu trojici kdy nerovnost neplatí
1) 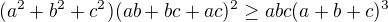 -> ideálně bez roznásobování závorek
-> ideálně bez roznásobování závorek
2) ![kopírovat do textarea $a+b+c \ge \sqrt[a+b+c]{a^ab^bc^c} + \sqrt[a+b+c]{a^bb^cc^a} + \sqrt[a+b+c]{a^c b^a c^b}$](/mathtex/37/3728db3fe53e4f5a73aeb7c3dadfe466.gif)
nebo ekvivalentní nerovnost
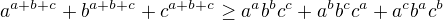
Jestli tyto nerovnosti platí, pak bych byl vděčný za nějaký "návod" jak se podobné nerovnosti dokazují. Já kdybych si je neodvodil tak asi moc nevím. Opravdu netuším, jak bych postupoval. V druhé nerovnosti bych možná položil 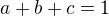 a první bych zkusil roznásobit... Což však podle mě k ničemu nevede.
a první bych zkusil roznásobit... Což však podle mě k ničemu nevede.
edit: Druhá z nerovností poté co jsem napsal její změněnou podobu vypadá že by šla celkem dobře dokázat za pomoci permutační nerovnosti. To mě teď napadlo. U te první mě ale pořád nic nenapadá.
Moje odvození:
Offline
#2 02. 06. 2014 18:47 — Editoval nikoma (02. 06. 2014 18:49)
Re: nerovnosti
Zdravím, zde nabídnu dva důkazy první nerovnosti
Offline
#3 02. 06. 2014 18:55 — Editoval liamlim (02. 06. 2014 18:59)
Re: nerovnosti
↑ nikoma:
Pěkné. Jen ještě ukážu nerovnost, jejíž speciálním případem je tato nerovnost. Pro kladná 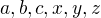 platí nerovnost
platí nerovnost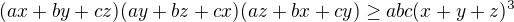
Volbou  ,
, 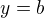 ,
,  získáme tu nerovnost. Sem jsem ji napsal jestli si dobře vzpomínám krátce poté co jsem tento obecný tvar odvodil. Nenapadlo mě nic lepšího než dosadit za
získáme tu nerovnost. Sem jsem ji napsal jestli si dobře vzpomínám krátce poté co jsem tento obecný tvar odvodil. Nenapadlo mě nic lepšího než dosadit za 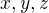
 . Myslím si, že jiným dosazením by šlo získat pěknější nerovnosti. Mimochodem podobná nerovnost kterou jsem dokázal je (zase stačí roznásobit)
. Myslím si, že jiným dosazením by šlo získat pěknější nerovnosti. Mimochodem podobná nerovnost kterou jsem dokázal je (zase stačí roznásobit)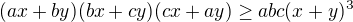 -> ta lze využít u nerovnosti kterou jsem tu nedávno napsal.
-> ta lze využít u nerovnosti kterou jsem tu nedávno napsal.
pro připomenutí ji sem napíšu: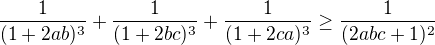
Offline
#4 02. 06. 2014 19:11 — Editoval nikoma (02. 06. 2014 19:22)
Re: nerovnosti
↑ liamlim:
To je pěkná nerovnost, docela mě překvapilo, že se jedná o přímý důsledek Hölderovy nerovnosti, protože podle Hölderovy nerovnosti platí
Analogicky jde odvodit i ta druhá nerovnost ve čtyrech proměnných.
EDIT: Ať to tu zbytečně nespamuju novým příspěvkem, tak jen dodám, že i ta obecná nerovnost pro 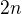 proměnných plyne obdobně z Hölderovy nerovnosti.
proměnných plyne obdobně z Hölderovy nerovnosti.
Offline
#5 02. 06. 2014 19:16 — Editoval liamlim (02. 06. 2014 19:26)
Re: nerovnosti
↑ nikoma:
Ono jde ukázat že platí
 tak
tak 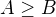
Ale už pro  nevypadá nerovnost vůbec hezky
nevypadá nerovnost vůbec hezky
Edit.: důkaz jsem dělal pomocí Jensenovy nerovnosti
Edit2: A ten důkaz není ani nijak zajimavy. Jedna se o stejny dukaz jako dukaz AG nerovnosti. Akorat s jinymi koeficienty. Pokud dosadíte 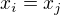 pak dostanete AG...
pak dostanete AG...
Offline
#6 09. 06. 2014 16:03
Re: nerovnosti
liamlim napsal(a):
Dokažte následující nerovnosti pro kladná
,
,
, nebo nalezněte alespoň jednu trojici kdy nerovnost neplatí
1)-> ideálně bez roznásobování závorek
Zdravím, podařilo se mi odvodit a dokázat silnější verzi této nerovnosti:
Dokažte, že pro kladná  platí
platí
Offline

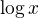 je rostoucí konkávní. Zároveň platí:
je rostoucí konkávní. Zároveň platí: 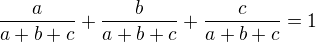 pro libovolná kladná
pro libovolná kladná ![kopírovat do textarea $\log\left( \frac{a^2+b^2+c^2}{a+b+c} \right) \ge \frac{a\log a + b\log b + c\log c}{a+b+c} = \log(\sqrt[a+b+c]{a^ab^bc^c})$](/mathtex/08/08ecdafc0d1ad831285223a04902c296.gif) . Protože je logaritmus rostoucí, můžeme nerovnost odlogaritmovat. Obdržíme nerovnost
. Protože je logaritmus rostoucí, můžeme nerovnost odlogaritmovat. Obdržíme nerovnost![kopírovat do textarea $\frac{a^2+b^2+c^2}{a+b+c} \ge \sqrt[a+b+c]{a^ab^bc^c}$](/mathtex/6b/6bd00b57268878030ee1060d1005be03.gif)
![kopírovat do textarea $\frac{ab+bc+ac}{a+b+c} \ge \sqrt[a+b+c]{a^bb^cc^a}$](/mathtex/04/042f22075a5ff8d8faa3cccc67b44b2d.gif)
![kopírovat do textarea $\frac{ab+bc+ac}{a+b+c} \ge \sqrt[a+b+c]{a^cb^ac^b}$](/mathtex/8c/8c970a85a154af792da410e61a77ad34.gif)
 ,
, 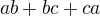 ,
, 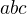 , pak se bude zřejmě jednat o nerovnost lineární v
, pak se bude zřejmě jednat o nerovnost lineární v  , v tomhle případě je nerovnost zřejmá.
, v tomhle případě je nerovnost zřejmá.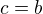 , navíc dokazovaná nerovnost je po substituci
, navíc dokazovaná nerovnost je po substituci  , poté nerovnost přejde do tvaru , což je pravda, protože , což vskutku platí, protože první nerovnost přejde po pokrácení do tvaru , což je Cauchy-Schwarzova nerovnost a druhá nerovnost přejde do tvaru , což snad není takový zločin roznásobit do tvaru . Jsme tedy hotovy.
, poté nerovnost přejde do tvaru , což je pravda, protože , což vskutku platí, protože první nerovnost přejde po pokrácení do tvaru , což je Cauchy-Schwarzova nerovnost a druhá nerovnost přejde do tvaru , což snad není takový zločin roznásobit do tvaru . Jsme tedy hotovy.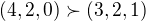 a
a 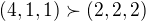 .
.