Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2014 21:03
Rovnice kuželoseček
Mám tu spoustu příkladů typu: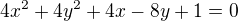 je rovnicí = kružnice
je rovnicí = kružnice
Na výběr, je vždy kružnice, parabola, hyperbola a elipsa. Formát zadání je vždy stejný. Lze rovnice nějak vždy upravit a spolehlivě poznat o jakou se jedná?
Děkuji za pomoc!
Offline
- (téma jako vyřešené označil(a) xdobia09)
#2 02. 04. 2014 21:15
Re: Rovnice kuželoseček
Samozřejmě, každá kuželosečka lze zapsat ve tvaru:
Pokud máš nějaký určitý typ této rovnice, musíš se snažit jí upravit na středový tvar. Dále by ti také mohlo pomoct to, že:
pokud je jedna ze dvou neznámých v druhé mocnině a ta zbývající ne, jedná se pravděpodobně o parabolu
pokud jsou obě neznámé v druhé mocnině, ale u jedné z nich je opačné znaménko, jedná se pravděpodobně o hyperbolu
pokud jsou obě neznáme v druhé mocnině, obě mají stejné znaménko (+ +) (- -) tak rozlišujeme dva typy:
mají stejný koeficient = kružnice
mají rozdílný koeficient = elipsa
Tvoje kuželosečka by se dala upravit následovně: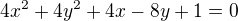

doplníme na čtverec: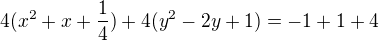


Jedná se tedy o kružnici se středem v bodě ![kopírovat do textarea $[-\frac{1}{2};1]$](/mathtex/d9/d99347affba36f47d74334dbec276531.gif) a poloměrem 1.
a poloměrem 1.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 02. 04. 2014 21:23
Re: Rovnice kuželoseček
↑ xdobia09:
koeficienty u kvadratických členů jsou stejné (i se znaménky) -> podezřelá je kružnice
koeficienty u kvadratických členů nejsou stejné ale mají stejná znaménka -> podezřelá je elipsa
koeficienty u kvadratických členů mají opačná znaménka -> podezřelá je hyperbola
je tam jen jeden kvadratický člen -> podezřelá je parabola
vše za předpokladu, že v rovnici není smíšený člen 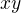 .
.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 02. 04. 2014 22:39 — Editoval vanok (02. 04. 2014 22:49)
Re: Rovnice kuželoseček
Ahoj ↑ zdenek1:
Mala poznamka:
Ako si spravne naznacil vyraz 
umoznuje urcit kuzelosecku v pripade ked c=0.
Tiez, ze vdaka vhodnemu otoceniu, mozme transformovat danu rovnicu kuzelosecky "na formu bez xy"
Ale naviac plati aj tento vysledok pre formu  :
:
Ak  mame rovnicu elipsy ( pripadne kruznice) alebo bodu alebo
mame rovnicu elipsy ( pripadne kruznice) alebo bodu alebo 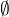
ak  mame rovnicu hyperboly alebo zjednotenia dvoch roznobeznych priamok
mame rovnicu hyperboly alebo zjednotenia dvoch roznobeznych priamok
a ak 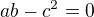 ide rovnicu paraboly alebo jednej priamky alebo dvoch rovnobeznych priamok alebo
ide rovnicu paraboly alebo jednej priamky alebo dvoch rovnobeznych priamok alebo 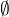
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 02. 04. 2014 23:12
Re: Rovnice kuželoseček
↑ vanok:
Zdravím, co za útvary může rovnice 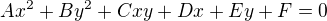 generovat?
generovat?
Klasicky - kružnice, elipsa, parabola, hyperbola.
Dál jsem zjistil, že to může být přímka, dvojice (různoběžných, nebo rovnoběžných) přímek, jeden bod nebo prázdná množina.
Ještě něco, nebo mám vše?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 02. 04. 2014 23:30 — Editoval vanok (02. 04. 2014 23:32)
Re: Rovnice kuželoseček
↑ byk7:,
To su tzv degenerovane pripady.
Pozor v klasifikacii som pouzil co bolo napisane v predoslych prispevkoch: !..
!..
Priklad na bod
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
