Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 04. 2014 23:41 — Editoval Makakpo (05. 04. 2014 23:58)
Spojitost a diferencovatelnost.
Ahoj, mame vetu: Funkcia je spojita v kazdom bode, v ktorom je diferencovatelna.
Ako to dokazat?
Ja by som mozno skusil nejako cez limitu, najprv dokazat ze kazda diferencovatelna funkcia v bode x ma limitu v bode x, a potom uz len dokazat ze kazda funkcia ktora ma limitu v bode x je v bode x aj spojita. Dobry/zly postup? Prosim navrhy, dakujem.
Offline
#2 05. 04. 2014 23:58 — Editoval jarrro (06. 04. 2014 00:18)
Re: Spojitost a diferencovatelnost.
existencia limity v ktorej vystupuje nejaká funkcia ešte nezaručuje existenciu limity tej funkcie
napríklad 
pritom Dirichletova funkcia nikde limitu nemá
a limitu môžu mať aj nespojité funkcie zober si napríklad
MATH IS THE BEST!!!
Offline
#5 06. 04. 2014 00:37
Re: Spojitost a diferencovatelnost.
Tvoju vetu prepis trocha inac
Ak f je derivatelna v bode x ( hypoteza)
tak potom
f je spojita v bode x. ( konluzia)
Poznamka: vzorec od kolegu ↑ jarrro: , napr tento ti moze posluzit ( je lahko dokazatelny pre kazde nenulove h)
Napis tvoju hypotezu a konkluziu v jazyku limit.
Skus. Pokracovanie dokazu zajtra.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 06. 04. 2014 10:59
Re: Spojitost a diferencovatelnost.
↑ Makakpo:tak že ju priamo dokazujú stačí na obidve strany aplikovať limitu
MATH IS THE BEST!!!
Offline
#9 06. 04. 2014 11:45 — Editoval vanok (06. 04. 2014 11:51)
Re: Spojitost a diferencovatelnost.
Hypoteza:
f je derivatelna v x
To sa ekvivalnte da povedat
*Existuje
* 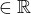
* a je 
*
Konkluzia
To sa da vyjadrit takto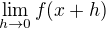
*Je 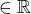
* a je 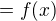
Tak vyuzi tuto rovnost od Jarra  aby z hypotezy si dokazal konkluziu.
aby z hypotezy si dokazal konkluziu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 06. 04. 2014 13:57 — Editoval vanok (06. 04. 2014 13:58)
Re: Spojitost a diferencovatelnost.
Vies  + hypotezu+ vety o limitach
+ hypotezu+ vety o limitach
Rovnost co plati ( pre nenulove h) plati aj pre limitu kazdej strany rovnosti.
To da.
Pokracuj, ta limita na druhej strane sa da rozpisat na tri limity ...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

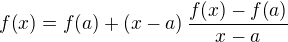
 znamená, že
znamená, že
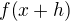 dosadíš
dosadíš  a použiješ základné vety o limitách tak ti to vyjde
a použiješ základné vety o limitách tak ti to vyjde