Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 08. 2014 16:10
Delitelnost polynomov
Dalsie cvicenie
Nech ![kopírovat do textarea $P \in\mathbb{K} [X]$](/mathtex/69/6959416cda8ba9c4d525dec578349db1.gif) , kde
, kde  je komutativne teleso.
je komutativne teleso.
Dokazte, ze 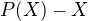 deli
deli 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 15. 08. 2014 21:50
#3 15. 08. 2014 22:38
Re: Delitelnost polynomov
Ahoj ↑ check_drummer:,
Tvoj dokaz plati v algebrickych uzavretych telesach.... Ale mozes to dokazat aj v inych pripadoch?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 16. 08. 2014 12:45
Re: Delitelnost polynomov
Cesta k jednemu dokazu:
Mozte poznamenat ze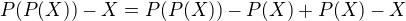 ...
...
Pozor na oznacenia 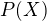 oznacuje polynom,
oznacuje polynom,
a 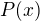 oznacuje hodnotu asociovanej polynomialnej funkcie
oznacuje hodnotu asociovanej polynomialnej funkcie
 k polynomu
k polynomu 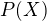 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 18. 08. 2014 12:58 — Editoval vanok (18. 08. 2014 13:01)
Re: Delitelnost polynomov
Dam aj koniec tohto dokazu, akoze algebristi su asi na prazdninach.
Je jasne ze staci dokazat ze 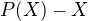 deli
deli  .
.
Ak  je nenulovy mozme pisat
je nenulovy mozme pisat  kde
kde 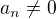 a tak
a tak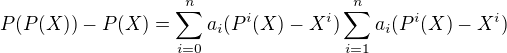
Pre  je lahke ukazat, ze
je lahke ukazat, ze  deli
deli 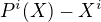 .
.
To da 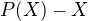 deli
deli  .
.
A toto ukoncuje dokaz.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
