Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 10. 2012 22:01
tělesa
Za domácí úkol na lineární algebru máme vymyslet nějaká tělesa a při přemýšlení mě napadl takový problém. Šlo by dokázat, že lze sestrojit těleso, které by obsahovalo čísla e a π (popřípadě libovolná dvě transcendentní čísla s určitými podmínkami) a zároveň neobsahovalo žádné racionální číslo?
Offline
#2 14. 10. 2012 11:39
- OiBobik
- Moderátor
- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: tělesa
↑ o.neill:
Ahoj,
no, tak triviální hloupá odpověď - když si vymyslíš správné operace, určitě to půjde. : )) (prostě uděláš dvouprvkové těleso, kde jeden prvek bude neutrální vůči aditivní operaci a druhý vůči multiplikativní operaci.)
Tebe to ale spíš asi zajímá jako podtěleso známého tělesa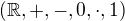 
, tj. chtěl bys na něm sčítat a násobit "přirozeně". To pak samozřejmě nejde, třeba už jen proto, že v takovém tělese musí být 
a 
.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 14. 10. 2012 12:15
Re: tělesa
No jo, to je fakt, tak nic no. Vím, že tělesa mohou být různě obskurní, ale na škole nám definovali těleso pouze jako podmnožinu C s „normálním“ sčítáním a odčítáním, takže jsem přemýšlel o těchto.
Offline
#4 14. 10. 2012 14:34
- OiBobik
- Moderátor
- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: tělesa
↑ o.neill:
Btw: můžeš si zkusit rozmyslet, že dokonce v každém takovém tělese (tzn. v podtělese komplexních čísel) budou nutně obsažena všechna racionální čísla.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 11. 09. 2014 19:00
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: tělesa
ahoj ↑ o.neill:,
myšlenkou ↑ OiBobik: by sis ale mohl šplhnout. Místo jednoho tělesa jste vymysleli úlohou:
Dokažte, že každé těleso (s běžně chápaným sečítáním a násobením) obsahující e, obsahuje také všechna racionální čísla.
A spolužáci, snažte se :-)
Budoucnost patří aluminiu.
Offline
#6 14. 09. 2014 20:42
Re: tělesa
Ahoj,
Aj ine telesa su ti iste pristupne,
Teleso algebrickych cisiel
Teleso p-adickych cisiel
Teleso quaternionov ....
a mnoho inych.
Pozri napr. na anglicku wikipediu.
Poznamka: vymysliet nejake teleso co nikto nepozna ( ako sa da rozumiet v tvojej uvodnej otazke) je iste velmi tazke...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline