Matematické Fórum

stuart clark · 05. 03. 2015 05:33

Let $n_{1}<n_{2}<n_{3}<n_{4}<n_{5}$ be positive integers such that $n_{1}+n_{2}+n_{3}+n_{4}+n_{5}=20.$

Then no. of distinct arrangement of 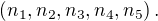$\left(n_{1},n_{2},n_{3},n_{4},n_{5}\right).$ is

byk7 · 09. 03. 2015 22:45 — Editoval byk7 (09. 03. 2015 23:22)

Note $n_i=m_i+i$ , where $1\le i\le5$ and $0\le m_1\le m_2\le\cdots\le m_5$ (1).
Thus we have equation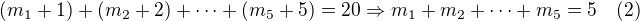
$$m_1+1$+$m_2+2$+\cdots+$m_5+5$=20 \Rightarrow m_1+m_2+\cdots+m_5=5\quad(2)$

So your question is equivalent to "how many solutions has the equation (2) satisfying condition (1)?"
And for an answer use Burnside's lemma.

Or you can just write down all cases, because
$\begin{matrix} m_1 & m_2 & m_3 & m_4 & m_5 \\ 0 & 0 & 0 & 0 & 5 \\ 0 & 0 & 0 & 1 & 4 \\ 0 & 0 & 0 & 2 & 3 \\ 0 & 0 & 1 & 1 & 3 \\ 0 & 0 & 1 & 2 & 2 \\ 0 & 1 & 1 & 1 & 2 \\ 1 & 1 & 1 & 1 & 1 \end{matrix}$
So we have 7 suitable 5-tuples.

(They are
$$n_1,n_2,n_3,n_4,n_5$\in\{(1,2,3,4,10),(1,2,3,5,9),(1,2,3,6,8),\color{white}\}$
$\color{white}\{\color{black}(1,2,4,5,8),(1,2,4,6,7),(1,3,4,5,7),(2,3,4,5,6)\}$ .)

stuart clark · 10. 03. 2015 04:06

Thanks ↑ byk7: for Nice explanation.

Matematické Fórum

#1 05. 03. 2015 05:33

no. of distinct arrangements

#2 09. 03. 2015 22:45 — Editoval byk7 (09. 03. 2015 23:22)

Re: no. of distinct arrangements

#3 10. 03. 2015 04:06

Re: no. of distinct arrangements

Zápatí