Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diskrétka - Indukce - Dolní/horní celá část (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 03. 2015 14:23
- lukki007

- Zelenáč
- Příspěvky: 4
- Škola: UJEP, PřF - Fyz. Mat.
- Pozice: Specialista pro reporting
- Reputace: 0
Diskrétka - Indukce - Dolní/horní celá část
Zdravím, dostal jsem za domácí úlohu důkaz platnosti tvrzení, ale nevím jak začít. Hádám, že by se na to dala použít indukce, ale nevím přesně jak ji využít, proto bych chtěl někoho poprosit o "nakopnutí" jak na to a zbytek bych třeba dopočítal a postnul já.
Které z následujících tvrzení platí pro všechna kladná reálná čísla x?
(a)
(b)
(c)
Pro a-c bych měl dokázat že platí pro všechna x, nebo alespoň pro jedno neplatí. (Experimentálně-dosazováním, jsem to již zjistil, ale potřeboval bych se na to podívat obecně.)
Díky,
Petr
Jinak jsme probírali tuto kapitolu, Kapitola 1.2.4 - Celočíselné funkce a teorie čísel z Donalda Knutha, Umění programování.
Offline
- (téma jako vyřešené označil(a) byk7)
#3 29. 03. 2015 15:03 — Editoval byk7 (29. 03. 2015 15:26)
Re: Diskrétka - Indukce - Dolní/horní celá část
Tak třeba a):
Pro jednoduchost zápisu označme  , kde
, kde  a
a  . Číslo
. Číslo  můžeme jednoznačně zapsat jako
můžeme jednoznačně zapsat jako  kde
kde 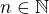 a
a  (tj.
(tj.  ). Pak zřejmě
). Pak zřejmě  , takže
, takže  .
.
Nyní chceme ukázat, že také  . Protože
. Protože  a
a  tak také
tak také  . Opět máme, že
. Opět máme, že  ,
,
což je požadovaný závěr, tj.  .
.
S b) to bude podobné, použiju stejné značení. Pokud je  celé, pak tvrzení platí triviálně. Dále předpokládejme, že
celé, pak tvrzení platí triviálně. Dále předpokládejme, že  . Pro čísla
. Pro čísla  , která nejsou celá platí
, která nejsou celá platí 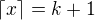 , chceme tedy ukázat, že
, chceme tedy ukázat, že  , zřejmě platí
, zřejmě platí  , takže
, takže  . Naopak platí
. Naopak platí  .), tzn.
.), tzn.  a jsme hotovi.
a jsme hotovi.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#4 29. 03. 2015 20:05
- lukki007

- Zelenáč
- Příspěvky: 4
- Škola: UJEP, PřF - Fyz. Mat.
- Pozice: Specialista pro reporting
- Reputace: 0
Re: Diskrétka - Indukce - Dolní/horní celá část
Díky moc byk7 za tak rychlou reakci.
Celkově jsem to snad pochopil, ale není mi jasné vyjádření dolní celé části ( ). Mohl bys přidat komentář, abych pochopil jak se to celé číslo dá zapsat jako
). Mohl bys přidat komentář, abych pochopil jak se to celé číslo dá zapsat jako  ? A klidně i nějakou literaturu, kde bych se o tom mohl dozvědět víc. Díky!
? A klidně i nějakou literaturu, kde bych se o tom mohl dozvědět víc. Díky!
byk7 napsal(a):
... Číslo
můžeme jednoznačně zapsat jako
kde
a
(tj.
)...
Offline
#5 29. 03. 2015 20:19
Re: Diskrétka - Indukce - Dolní/horní celá část
Proč to jde? Podle mě je to "zřejmé"
1=1^2+0
2=1^2+1
3=1^2+2
4=2^2+0
5=2^2+1
6=2^2+2
7=2^2+3
8=2^2+4
9=3^2+0
10=3^2+1
...
Prostě pro dané  najdeš vždy
najdeš vždy  takové, že
takové, že  . Pak je samozřejmě
. Pak je samozřejmě  a
a  . Nebo jinak každé číslo můžeš ohraničit nějakými dvěma druhými mocninami.
. Nebo jinak každé číslo můžeš ohraničit nějakými dvěma druhými mocninami.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diskrétka - Indukce - Dolní/horní celá část (TOTO TÉMA JE VYŘEŠENÉ)


