Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 12. 2015 22:32
Minimální kostra
Dobrý večer,
rád bych se zeptal, jak se řeší následující typ úloh, protože jsem jich moc (víceméně jenom zadání) nenašel, tak se ptám tady.
Mám úplný graf 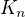 kde
kde  a ohodnocení hran, které je následující
a ohodnocení hran, které je následující  .
.
Mám najít váhu minimální kostry
Zde je to ještě jednoduché, protože nějakou intiucí můžu dojít k tomu, že kostra 1,2,...,n jistě bude kostrou, která je zároveň stromem (isomorfní cestě Pn) a součet vah bude jistě nejmenší, protože pokud bych začal hledat kostru (pomocí Jarníkova algrotimu), tak vyjdu z bodu 1, nejlevnější hrana je do 2, odtamtud do 3 atd.
Nicméně můj dotaz je spíš, když je zadání stejné, nicméně ohodnocení hran je následující:
Zde netuším, jak je to myšleno, protože  je množina. Je to tedy to samé, jako
je množina. Je to tedy to samé, jako  , takže pro jednu hranu bych měl mít váhu
, takže pro jednu hranu bych měl mít váhu  ?
?
A když by to bylo nějak jasně dané, řekněme, že se bere větší z těch možných hodnot, jak by se tedy postupovalo?.
Děkuji předem za nápady
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 20. 12. 2015 19:14
Re: Minimální kostra
Já myslím, že příklad není korektně zadaný. Váha hrany závisí na konkrétním označení, což není v pořádku.
Buďme shovívaví a dejme tomu, že bereme v větší než u. Potom bych ale řekl, že nejmenší příspěvek do váhy budou mít ty hrany, kde první vrchol je vždy u=1 a druhý vrchol je v=2,..n. Kostru bych proto čekal jako hvězdu, nikoliv cestu (mimochodem stejně u prvního příkladu.)
Zkusil bych zdůvodnit pomocí nerovnic s parametry u,v.
Offline
#5 20. 12. 2015 21:40
Re: Minimální kostra
jojo toto mě také napadlo, že by se musela brát jednička pro to "u".
Jinak díky aspoň že příspěvek ;) příklad není korektně zadaný, což není správné.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
