Matematické Fórum

liamlim

Ahoj. Mám dotaz ohledně počítání součtů řad. Prosím o radu, jak by šlo "rozumně" přijít například na to, že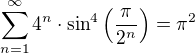

$\sum_{n=1}^\infty4^n\cdot\sin^4\left(\frac{\pi}{2^n}\right) = \pi^2$

Totiž takto, jsem v prváku a součty řad jsme ještě vůbec nedělali, jenom mě velmi fascinují. Proto mi jde spíš než o úplně dokonale matematicky správné zdůvodnění klidně i ne úplně formálně správné navedení, jak se vlastně podobné věci počítají.

Já jsem si tento součet (asi ne úplně matematicky správně) spočítal tak, že jsem upravoval 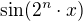$\sin(2^n\cdot x)$ pomocí vztahu pro sinus dvojnásobného úhlu tak, abych se všech kosinů po cestě zbavil. Tím jsem došel k tomu, že

$\sum_{n=1}^\infty4^n\cdot\sin^4\left(\frac{\pi}{2^n}\right) = \lim_{n\to \infty}4^n\cdot\sin^2\left(\frac{\pi}{2^n}\right)= \pi^2$

Proč tento text píšu, když jsem sám spočítal součet řady? Protože vím, že bych ho nespočítal. Já jsem nevěděl vůbec o takové řadě, jen jsem si upravoval 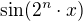$\sin(2^n\cdot x)$ a ta řada tak nějak sama vyplynula. Kdybych naopak například v testu měl součet uvedené řady počítat tak jsem naprosto ztracený. Proto se ptám. Díky!

EDIT:

Naprosto podobně jsem si teď odvodil součet řady s třetími mocninami. Nevíte někdo o nějakém zobecnění? Nebo způsobu jak by se dal v rozumném čase součet spočítat? Zajímalo by mě to.

$\sum_{n=1}^\infty 3^n\cdot\sin^3\left(\frac{\pi}{3^n}\right) = \frac{3}{4}\cdot\lim_{n\to\infty}3^n\cdot\sin\left(\frac{\pi}{3^n}\right) = \frac{3}{4}\cdot\pi$

Rumburak

↑ liamlim:

Ahoj.

Je mnoho konvergentních řad, které sečíst se ještě nikomu nepodařilo. Stává se i to, že někdo řeší nějaký
úplně jiný matematický problém a součet nějaké konkretní řady pak z toho vyjde jako "bonus".

Další možností je nahradit některou konstatu proměnnou a zkoumat tzv. řadu funkcí, zde například

$\sum_{n=1}^\infty x^n\cdot\sin^x\left(\frac{\pi}{2^n}\right)$ .

(Ale jde opravdu jen o ilustrační příklad, nikoliv o návod, který by zde zaručeně vedl k cíli). Není těžké dokázat,
že tato řada konverguje pro $x \in \langle 0, 1 \rangle$ . Jejím součtem pak je $f(x)$ , kde $f$ je neznámá funkce, kterou
chceme určit. Vyšetřováním vlastností takto definované funkce se nám mohou otevřít další cesty postupu.
(Například řadu složenou z funkcí lze za určitých předpokladů derivovat "člen po členu" a pod.)
Konkretní radu ale nabídnout neumím. Obecné pravidlo, jak sčíítat všechny konvergentní řady, zatím neexistuje. :(

Pavel · 29. 01. 2016 13:44

↑ liamlim:

Identity a postupy, které uvádíš, jsou jednoduché, nicméně dávají hezké výsledky. Bez znalosti triku využívajícího hodnoty sinu v násobcích x netuším, jak by se obě uvedené řady daly sečíst. Možná prostředky komplexní analýzy, ale to jen odhaduji. Dokonce to netuší ani Mathematica v. 10.0.3.. Obecná metoda pro sčítání nekonečných řad není k dispozici. Často je způsob právě opačný - různými postupy se, jako ve Tvém případě, nekonečná řada vytvoří. Odborníkem na to je kolega Marian :-)

Jinak takové elementární nekonečné řady už nedostaneš použitím vzorců pro sinus čtyř a vícenásobného argumentu. Postup bude fungovat i nadále, ale počet členů, které se sčítají, bude v nekonečné řadě postupně narůstat.

Obdobné postupy, resp. nekonečné řady, lze použít, resp. vytvořit, i pomocí tzv. hyperbolických funkcí, pro něž existují velmi podobné identity týkající se jejich hodnot s násobným argumentem.

Bati · 30. 01. 2016 00:52

Ahoj ↑ liamlim:,
jak jsi to prosím odvodil? Jak se zbavíš těch kosinů?

liamlim

↑ Bati:

Ahoj,

$\sin(2^n\cdot x) = 2\sin(2^{n-1}\cdot x)\cos(2^{n-1}\cdot x)$
$\sin^2(2^n\cdot x) = 4\sin^2(2^{n-1}\cdot x)\cos^2(2^{n-1}\cdot x)$
$\sin^2(2^n\cdot x) = 4\sin^2(2^{n-1}\cdot x)(1-\sin^2(2^{n-1}\cdot x))$
$\sin^2(2^n\cdot x) = 4\sin^2(2^{n-1}\cdot x) - 4\sin^4(2^{n-1}\cdot x)$

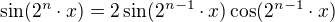
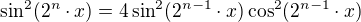
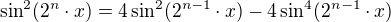
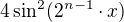A teď už jen dosazuji za $4\sin^2(2^{n-1}\cdot x)$ dokud se nedostanu k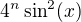 $4^n\sin^2(x)$

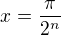Pro $x = \frac{\pi}{2^n}$ dostáváme vlevo 0. Odsud již plyne: $\sum_{n=1}^\infty4^n\cdot\sin^4\left(\frac{\pi}{2^n}\right) = \lim_{n\to \infty}4^n\cdot\sin^2\left(\frac{\pi}{2^n}\right)= \pi^2$