Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 02. 2016 22:55
- ninjashinobu1235

- Zelenáč
- Příspěvky: 6
- Škola: FEI Univerzita Pardubice
- Pozice: Student
- Reputace: 0
Cauchyůvho vzorec
Ahoj, potřeboval bych pomoct vyřešit tento příklad kdyby se opakoval na další zkoušce :)
Spočtěte:
kde  je kružnice
je kružnice 
Můj postup:
Je to příklad na cauchyův vzorec takže bych potřeboval tvar 
No, pokud by nebylo ve jmenovateli  , ale
, ale  tak bych to řešil takto:
tak bych to řešil takto:



a výsledek by tedy byl 
Problém je, že 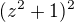 mi nejde nijak rozumně rozložit, protože
mi nejde nijak rozumně rozložit, protože  ani
ani  mi tu moc nepomůžou.
mi tu moc nepomůžou.
Offline
- (téma jako vyřešené označil(a) ninjashinobu1235)
#2 07. 02. 2016 11:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Cauchyůvho vzorec
Zdravím,
rozklad  , oba póly však jsou uvnitř oblasti, tedy nejspíš upravit na součet 2 (nebo více) integrálů tak, aby každý se vztahoval jen jednomu
, oba póly však jsou uvnitř oblasti, tedy nejspíš upravit na součet 2 (nebo více) integrálů tak, aby každý se vztahoval jen jednomu 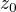 . S kolegou jsme diskutovali podobnou situaci, také se podívej do odkazu, jelikož se mi Tvůj Cauchy vzorec se zdá být správný. Stačí tak na úvod? Děkuji.
. S kolegou jsme diskutovali podobnou situaci, také se podívej do odkazu, jelikož se mi Tvůj Cauchy vzorec se zdá být správný. Stačí tak na úvod? Děkuji.
Offline
#3 07. 02. 2016 14:13 — Editoval ninjashinobu1235 (07. 02. 2016 16:17)
- ninjashinobu1235

- Zelenáč
- Příspěvky: 6
- Škola: FEI Univerzita Pardubice
- Pozice: Student
- Reputace: 0
Re: Cauchyůvho vzorec
Děkuji, nad rozkladem na i jsem nepřemýšlel, počítal bych to tedy takto:


Podle vzorce ![kopírovat do textarea $f(z)' = [\frac{u}{v}]' = \frac{u'v - uv'}{v^2}$](/mathtex/ef/ef9477c40c8fc5ec99031e804ba98680.gif)

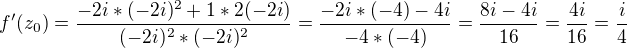
Výsledek by byl: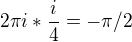
Je to správný postup? Děkuji.
Offline
#4 07. 02. 2016 16:04 — Editoval jelena (07. 02. 2016 16:29)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Cauchyůvho vzorec
↑ ninjashinobu1235:
děkuji, to asi nebude dobře, jelikož pořád v jednom kroku výpočtu pracuješ s oběma póly (musela by být taková úprava výrazu 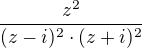 , která od sebe jednotlivé póly oddělí do samostatných integrálů (takovou úpravu do parciálních zlomků typů
, která od sebe jednotlivé póly oddělí do samostatných integrálů (takovou úpravu do parciálních zlomků typů 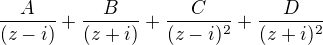 (edit: oprava jmenovatelů)
(edit: oprava jmenovatelů)
Což může být nadlouho (ale vyzkoušet můžeš). Druhá možnost je využití rozdělení oblasti (u nás kružnice se středem (0,0) a poloměrem 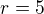 ) na uzavřené podoblasti tak, aby každý pol se dostal do své oblasti, která nezasahuje do oblasti druhého pólu, potom na každou oblast použit Cauchy vzorec (v materiálech byste měli mít k tomu platnou větu - důsledek). Narychlo nenajdu lepší použitelný obrázek, než tento v RJ: příklad 3-10 a obrázek 21 (je to i přesně případ Tvých pólů) Odkaz. Jinak postup budeš mít v pořádku, jen Tobě chybí stejnou techniku použit také na druhý pól. Zatím jsi pracoval jen s jedním (-i).
) na uzavřené podoblasti tak, aby každý pol se dostal do své oblasti, která nezasahuje do oblasti druhého pólu, potom na každou oblast použit Cauchy vzorec (v materiálech byste měli mít k tomu platnou větu - důsledek). Narychlo nenajdu lepší použitelný obrázek, než tento v RJ: příklad 3-10 a obrázek 21 (je to i přesně případ Tvých pólů) Odkaz. Jinak postup budeš mít v pořádku, jen Tobě chybí stejnou techniku použit také na druhý pól. Zatím jsi pracoval jen s jedním (-i).
Ještě k zápisu (už jsem pochopila, že znakem  neznačíš produkt, ale jen \pi (
neznačíš produkt, ale jen \pi ( ). Nemáte váš materiál online? Děkuji.
). Nemáte váš materiál online? Děkuji.
Offline
#5 07. 02. 2016 16:23
- ninjashinobu1235

- Zelenáč
- Příspěvky: 6
- Škola: FEI Univerzita Pardubice
- Pozice: Student
- Reputace: 0
Re: Cauchyůvho vzorec
Děkuji za pomoc, 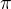 jsem v druhém příspěvku opravil(první nejde editovat) a omlouvám se za zmatky, přehlédl jsem ho v nabídce LaTeXového editoru. Materiál bohužel online nemám.
jsem v druhém příspěvku opravil(první nejde editovat) a omlouvám se za zmatky, přehlédl jsem ho v nabídce LaTeXového editoru. Materiál bohužel online nemám.
Offline
#6 07. 02. 2016 16:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Cauchyůvho vzorec
↑ ninjashinobu1235:
materiál - nevadí, že není (určitě v něm tvrzení ohledně využití rozdělení na oblasti budete mít) - něco v takovém smyslu - kap.2.2. K řešení - můžeš odzkoušet jak parciální zlomky (ještě jsem opravila první 2 jmenovatele), nebo přímo důsledek Cauchy věty (teorie + RJ materiál by to měl projasnit dostatečně).
Offline
#7 07. 02. 2016 17:30
- ninjashinobu1235

- Zelenáč
- Příspěvky: 6
- Škola: FEI Univerzita Pardubice
- Pozice: Student
- Reputace: 0
Re: Cauchyůvho vzorec
↑ jelena:
Děkuji.
Offline