Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 03. 2016 17:41 — Editoval vanok (03. 03. 2016 23:40)
Rada
Pozdravujem,
Najdite jeden polynom  taky, ze
taky, ze ![kopírovat do textarea $ u_n=\sqrt {n^4+ 2n^2}-\sqrt[3]{P(n)}$](/mathtex/88/88a1826f3e793ba7b6c11843ecfde402.gif) je vseobecny clen jednej konvergentnej rady.
je vseobecny clen jednej konvergentnej rady.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 03. 03. 2016 23:43
Re: Rada
Ahoj ↑ Freedy:
Ide presne o tuto radu ![kopírovat do textarea $\sum_{n=1}^{\infty }\bigg(\sqrt{n^4+2n^2}-\sqrt[3]{P(n)}\bigg)$](/mathtex/16/16b04dccae4f4cd6a5af86414ab79d78.gif)
( opravil som preklep aj v prvom prispevku)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 04. 03. 2016 01:53 — Editoval Freedy (04. 03. 2016 01:55)
Re: Rada
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 04. 03. 2016 06:10
Re: Rada
Pozdravujem ↑ Freedy:,
Ty hras rad na hadanky?
Tak pridat dokaz by nebolo spatne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 04. 03. 2016 09:41 — Editoval Freedy (04. 03. 2016 19:40)
Re: Rada
↑ vanok:
Zde je moje řešení:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 04. 03. 2016 19:23
Re: Rada
Ahoj
To tvoje riesenie nie je velmi zrozumitelne ( i ked sa tam najde jedna, dve dobre myslienky) a je v nom vela nevysvetlenych pojmov.
A a tiez nie je jasny ani suvis z tvojim predoslym tvrdenim.↑ Freedy: ( ktore myslis, ze bolo uplne riesenie? )
Skus pouzit na riesenie asymptoticky rozvoj v okoli 
Tak dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 04. 03. 2016 19:42
Re: Rada
↑ vanok:
Ahoj,
Který konkrétní krok postupu ti přijde nesrozumitelný? :D
Je to špatné řešení?
A souvis s předešlým tvrzením? Vždyť jsem se dopracoval k naprosto stejnému výsledku :D
;-) asymptotické rozvoje sem tahat nepotřebuji (dle mého uvážení), stačí pouze srovnávací kritérium.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 04. 03. 2016 21:01 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Duplicity
#10 04. 03. 2016 21:04
Re: Rada
vanok napsal(a):
↑ Freedy:,
Tak ho dopln a vysvetli vsetko co si nevysvetlil.
Napr. Co to je totokde je to presne definovane?
Kde si dokazal presne tvoj posledny riadok?
A co zarucuje ze toto su vsetki riesenia ↑ Freedy:?
A preco sa bojis asymptotickych rozvojov? Kde sa da problem problem elegantne riesit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 04. 03. 2016 22:22 — Editoval Freedy (04. 03. 2016 22:25)
Re: Rada
Dobrá tedy,
mám řadu![kopírovat do textarea $\sum_{n=1}^{\infty }\bigg(\sqrt{n^4+2n^2}-\sqrt[3]{P(n)}\bigg)$](/mathtex/16/16b04dccae4f4cd6a5af86414ab79d78.gif)
a chci zjistit, pro jaký polynom P(n) tato řada konverguje.
V jmenovateli se vyskytuje pouze funkce ve tvaru 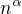 . (pokud teda neuvažujeme nekonečné polynomy, které můžou přecházet v různé funkce).
. (pokud teda neuvažujeme nekonečné polynomy, které můžou přecházet v různé funkce).
Pokud daný rozdíl rozšíříme, (jelikož se jedná o rozdíl polynomů) výrazem:![kopírovat do textarea $\frac{\sqrt{(n^4+2n^2)^5}+\sqrt{(n^4+2n^2)^4}\cdot \sqrt[3]{P(n)}+\sqrt{(n^4+2n^2)^3}\cdot \sqrt[3]{P^2(n)}+\sqrt{(n^4+2n^2)^2}\cdot \sqrt[3]{P^3(n)}+\sqrt{(n^4+2n^2)}\cdot \sqrt[3]{P^4(n)}+\sqrt[3]{P^5(n)}}{\sqrt{(n^4+2n^2)^5}+\sqrt{(n^4+2n^2)^4}\cdot \sqrt[3]{P(n)}+\sqrt{(n^4+2n^2)^3}\cdot \sqrt[3]{P^2(n)}+\sqrt{(n^4+2n^2)^2}\cdot \sqrt[3]{P^3(n)}+\sqrt{(n^4+2n^2)}\cdot \sqrt[3]{P^4(n)}+\sqrt[3]{P^5(n)}}$](/mathtex/5f/5f9a175fec435e7193ad77ed29dc964b.gif)
zkrátka rozšiřuji zlomek výrazem 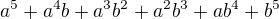 kde
kde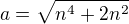
![kopírovat do textarea $b=\sqrt[3]{P(n)}$](/mathtex/e7/e72ca7a6de1fa5d26627cffc4ab05fd9.gif)
protože potom dostanu v čitateli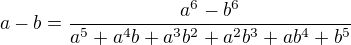
V čitateli tedy mám: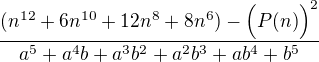
Vím, že 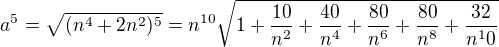 (ten součet 1 + ... to je to moje
(ten součet 1 + ... to je to moje  , proto to v dalším kroku už nebudu takhle rozepisovat, protože mě to nezajímá, jaké čísla tam jsou, důležité, že jdou k nule, když n jde k nekonečnu)
, proto to v dalším kroku už nebudu takhle rozepisovat, protože mě to nezajímá, jaké čísla tam jsou, důležité, že jdou k nule, když n jde k nekonečnu)
podobně u ostatních například:![kopírovat do textarea $a^4b=\sqrt{(n^4+2n^2)^4}\cdot \sqrt[3]{P(n)}=n^{8}\sqrt{1+P_{<0}(n)}\cdot n^{\frac{k}{3}}\sqrt[3]{1+Q_{<0}(n)}$](/mathtex/eb/eb82948f7fd24d51d7afa0b2a6d26009.gif)
kde  je stupeň polynomu
je stupeň polynomu 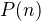 .
.
Nyní lze vzít do úvahy dvě věci.
V čitateli máme výraz: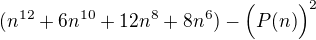
Pokud by stupeň polynomu P(n) byl větší než 6, pak se bude dát čitatel zapsat jako:
zatímco nejvyšší mocnina ve jmenovateli bude 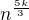 a tedy dokonce nebude ani splněna nutná podmínka konvergence pro řady.
a tedy dokonce nebude ani splněna nutná podmínka konvergence pro řady.
Proto musí být 
Pro  dostáváme, že potom se bude dát čitatel zapsat jako
dostáváme, že potom se bude dát čitatel zapsat jako  a nejvyšší mocnina jmenovatele bude
a nejvyšší mocnina jmenovatele bude 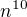 (větší tam vzniknout nemůže. A tedy zase nebude možné splnit nutnou podmínku konvergence.
(větší tam vzniknout nemůže. A tedy zase nebude možné splnit nutnou podmínku konvergence.
Z toho plyne, že stupeň polynomu musí být 6, tedy 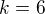 .
.
Pro k = 6 uvažme polynom  kde
kde
1) 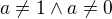
2) 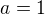
první případ je jednoduchý. Přejde to totiž opět na podobný případ jako s k=7. V čitateli zůstane  , ve jmenovateli bude nejvyšší mocnina
, ve jmenovateli bude nejvyšší mocnina 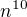 - opět není splněna podmínka konvergence.
- opět není splněna podmínka konvergence.
Když a = 1 tak se členy s  odečtou a zbyde v čitateli:
odečtou a zbyde v čitateli:
Nyní uvažme, zda-li by polynom mohl obsahovat člen:
A) 
kdyby obsahoval tento člen, tak potom se v umocněném polynomu na druhou objeví člen  , což by byl opět větší stupeň, než stupeň v jmenovateli.
, což by byl opět větší stupeň, než stupeň v jmenovateli.
B)  Tento člen tam být musí. Dokonce musí obsahovat koeficient 3. Proč? Protože v umocněném polynomu se objeví člen
Tento člen tam být musí. Dokonce musí obsahovat koeficient 3. Proč? Protože v umocněném polynomu se objeví člen 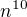 . Kdyby se koeficient u
. Kdyby se koeficient u  nerovnal 3, pak bude nejvyšší stupeň čitatele stále
nerovnal 3, pak bude nejvyšší stupeň čitatele stále 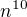 a stále nebude splněna nutná podmínka konvergence.
a stále nebude splněna nutná podmínka konvergence.
Musí se tedy vyskytovat s koeficientem 3, protože potom se odečtou členy 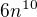 a právě člen
a právě člen 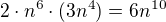 .
.
Jakmile se tyto dva členy odečetly, v čitateli už zůstává pouze 
Kdyby polynom P obsahoval člen 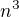 , pak by obsahoval i člen
, pak by obsahoval i člen  (jako součin
(jako součin  ). Kdyby se tam tento člen nacházel, pak čitatel má nejvyšší stupeň polynomu 9, tvar:
). Kdyby se tam tento člen nacházel, pak čitatel má nejvyšší stupeň polynomu 9, tvar:
a jmenovatel obsahuje pořád člen 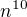 .
.
Jenže Taková řada, se dá celkem jednoduše srovnat s harmonickou řadou - která diverguje!.
Proto P nemůže obsahovat člen 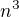 .
.
Pokud uvážíme členy  , kde
, kde 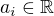 , pak tato řada diverguje.
, pak tato řada diverguje.
Proč?
Protože polynom P vypadá následovně: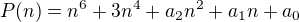
Po umocnění:
Členy  se odečtou a výsledky tvar zlomku bude následovný:
se odečtou a výsledky tvar zlomku bude následovný: .
.
Jen pro přenost teda závorka ve jmenovateli jde k vlastnímu, nenulovému číslu!!! (konkrétně k 5)
Proto 
řada konverguje, protože když ji srovnáme s řadou  dostáváme:
dostáváme:
Tato limita, nemůže vyjít nekonečno. Protože dole máme nanejvýš takový polynom jako v čitateli.
Proto podle lim. srovnávacího kritéria víme, že řada  musí konvergovat, protože jsme ji srovnali s konvergentní řadou a nevyšlo to nekonečno, ale číslo reálné.
musí konvergovat, protože jsme ji srovnali s konvergentní řadou a nevyšlo to nekonečno, ale číslo reálné.
↑ vanok:
pokud ale chceš, aby se hledal nekonečný rozvoj nějaké funkce taylorovým polynomem, tak by bylo dobré v úvodu říci, že jsou povolené i nekonečné polynomy.
Děkuji :)
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#12 04. 03. 2016 22:53
Re: Rada
↑ Freedy:
Poznamka. Polynom ma vzdy len konecny pocet clenov (vsak dobre vies ako sa definuje)
Co si napisal teraz vyzera o mnoho sympatickejsie. Precitam to zajtra.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 05. 03. 2016 15:26
Re: Rada
Ahoj ↑ Freedy:,
Ano teraz je to jasnejsie. No ale kolko prace.
Tu ti dam popis ako sa to tiez da urobit.
V okoli nekonecna mas 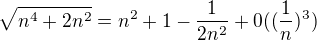
Hned vidis, ze mas trivialne riesenie pre  , taky ze
, taky ze 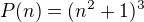
Pre priciny co su lahko ukazat, staci vysetrit chovanie polynomov  , takych, ze
, takych, ze 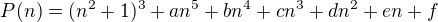 kde a,..,f su konstanty ktore su vhodne pre poziadavky cvicenia.
kde a,..,f su konstanty ktore su vhodne pre poziadavky cvicenia.
( cele riesenie teraz ma maxi 10 riadkov, aj so vsetkymi vysvetleniami)
Tak ci tak ti gratulujem, ze si napisal citatelnu verziu tvojho riesenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

![kopírovat do textarea $\sum_{n=1}^{\infty }\bigg(\sqrt{n^4+2n^2}-\sqrt[3]{P(x)}\bigg)$](/mathtex/78/78f719cb8d4d2dd40d27341bda1ac917.gif) konverguje
konverguje 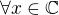 ?
? kde
kde 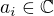 ,
, 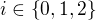
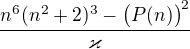
![kopírovat do textarea $\varkappa =\sqrt{(n^4+2n^2)^5}+\sqrt{(n^4+2n^2)^4}\cdot \sqrt[3]{P(n)}+\sqrt{(n^4+2n^2)^3}\cdot \sqrt[3]{P^2(n)}+\sqrt{(n^4+2n^2)^2}\cdot \sqrt[3]{P^3(n)}+\sqrt{(n^4+2n^2)}\cdot \sqrt[3]{P^4(n)}+\sqrt[3]{P^5(n)}$](/mathtex/11/1127dbce2b988e7ce97a215e5582e654.gif)
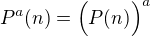
![kopírovat do textarea $\varkappa =n^{10}\cdot \bigg( \sqrt{1+P_{< 0}(n)}+\sqrt{1+P_{<0}(n)}\cdot \sqrt[3]{1+P_{<0}(n)}+...\bigg)$](/mathtex/62/6209c448beff9824aefe3dd6f6c88b5c.gif)

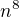 .
.