Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 05. 05. 2016 19:19
Re: Řešení Matematika+ 2016
↑ misaH:
http://www.novamaturita.cz/zadani-pisem … 38149.html
druhá je Matika+
Offline
#4 05. 05. 2016 19:21 Příspěvek uživatele 2pir byl skryt uživatelem 2pir.
#5 05. 05. 2016 20:31 — Editoval byk7 (05. 05. 2016 20:50)
Re: Řešení Matematika+ 2016
↑ anetkaj:
Je možné, že jsem někde udělal chybu, tak to ber s rezervou. :-)
1) 113
2) x=-3
3) n=179
4) 5
5) k=-15
6) 9 cm^2
7) 
8) bod C získáme okamžitě pomocí středové souměrnosti,
nad úsečkou AC sestrojíme množinu bodů, ze které můžeme
vidět tuto úsečku pod úhlem 60°, průsečíkem s p dostaneme bod(y) B
9) y=1
10) A=[-2,3], B=[6,7]
11)
12) b=1/4, b=a/(1-2a), s=1/3
13) B, E, C
14) D, F, A
15) E
16) A
17) D
18) B
19) B
20) C
21) C
22) D
23) A, A, A
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 05. 05. 2016 20:44 — Editoval extrander2 (05. 05. 2016 20:50)
- extrander2

- Zelenáč
- Příspěvky: 1
- Škola: gymnázium
- Pozice: student
- Reputace: 0
Re: Řešení Matematika+ 2016
3) není to spíš n = 179?
22) A co když se v těch 6 lidech, kteří umí daný jazyk, vyskytne dvojice, kde 1 umí jen francouzsky a druhý jen anglicky? Taková možnost může nastat. Takže podle mě bude pravděpodobnost menší.
Nešlo by to řešit tedy takto: 5 lidí umí anglicky - 5 nad 2 = 10 ... 3 lidí umí francouzsky - 3 nad 2 = 3 ... ale jsou zde 2 lidi, kteří umí jak anglicky, tak francouzsky, takže jsou zahrnuti 2x (viz diagram), je tedy potřeba odečíst 2 nad 2 = 1
Celkem tedy vyjde: (10 + 3 - 1) / (10 nad 2) = 12 / 45 = 4 /15 => D
Offline
#7 05. 05. 2016 20:50
Re: Řešení Matematika+ 2016
↑ extrander2:
Jistě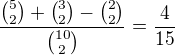
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#11 06. 05. 2016 10:20
- JuicyButtock

- Zelenáč
- Příspěvky: 1
- Pozice: Student
- Reputace: 0
Re: Řešení Matematika+ 2016
Mohu se zeptat, jaký je přesně postup řešení příkladu č. 19?
Offline
#13 06. 05. 2016 12:07
- lukyhruska96

- Zelenáč
- Příspěvky: 2
- Škola: SPŠ MB
- Pozice: student
- Reputace: 0
Re: Řešení Matematika+ 2016
Mohu se zeptat jak se řešila úloha č. 7? Já myslel, že nejkratší vzdálenost od přímky FH k bodu A je vzdálenost středu horní plochy od bodu A, tudíž mi vyšlo 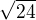
Offline
#14 06. 05. 2016 12:17 — Editoval gadgetka (06. 05. 2016 12:18)
Re: Řešení Matematika+ 2016
Ahoj, hledaná vzdálenost je úhlopříčkou obdélníku o stranách 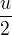 , kde u je úhlopříčka podstavy, a
, kde u je úhlopříčka podstavy, a  .
.
Edit: 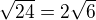 :D
:D
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#15 06. 05. 2016 12:30
- lukyhruska96

- Zelenáč
- Příspěvky: 2
- Škola: SPŠ MB
- Pozice: student
- Reputace: 0
Re: Řešení Matematika+ 2016
↑ gadgetka:
Ajo :D Jsem si to ani nezkusil naházet do kalkulačky, moje chyba :D Děkuju :)
Offline
#16 06. 05. 2016 13:27
- matematikaplus

- Zelenáč
- Příspěvky: 3
- Škola: Gymnázium u Libeňského zámku
- Pozice: Student
- Reputace: 0
Re: Řešení Matematika+ 2016
U úlohy 15, nemělo by to spíš bejt D? První rovnice sahá od intervalu <5,+nekonečno). Definiční obor se otáčí pouze v případě absolutní hodnoty nebo mínusu před logaritmem ne?
U úlohy 6, chci se zeptat proč je to 9 a ne 6?
Díky :)
Offline
#17 06. 05. 2016 13:50
Re: Řešení Matematika+ 2016
Ahoj, znak nerovnosti se mění, pokud je základ logaritmu z intervalu (0; 1), čili menší než 1.
Poměr uvedených stran je 6/4 = 1,5. U trojúhelníku s plochou 4 musí mít výška délku 2 cm, u většího trojúhelníku bude mít tedy výška délku 3 cm (2*1,5). Obsah pak bude:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#18 06. 05. 2016 13:52
- matematikaplus

- Zelenáč
- Příspěvky: 3
- Škola: Gymnázium u Libeňského zámku
- Pozice: Student
- Reputace: 0
Re: Řešení Matematika+ 2016
Díky :)
Offline
#22 07. 05. 2016 16:14
- matematikaplus

- Zelenáč
- Příspěvky: 3
- Škola: Gymnázium u Libeňského zámku
- Pozice: Student
- Reputace: 0
Re: Řešení Matematika+ 2016
Mohu se zeptat, jak vyřešit 10. a 12. Díky :)
Offline
#23 07. 05. 2016 20:53 — Editoval Al1 (07. 05. 2016 20:59)
Re: Řešení Matematika+ 2016
↑ matematikaplus:
Zdravím,
ad 10)  a pro souřadnice těžiště platí
a pro souřadnice těžiště platí ![kopírovat do textarea $T\bigg[\frac{x_{A}+x_{B}+x_{C}}{3}; \frac{y_{A}+y_{B}+y_{C}}{3}\bigg]$](/mathtex/0a/0a3c1cd03fcc85d7f440184206a8e85f.gif)
ad 12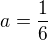 , pak první řada je geometrická s prvním členem
, pak první řada je geometrická s prvním členem  a koeficient
a koeficient  a její součet je
a její součet je 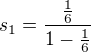
druhá řada je také geometrická s prvním členem b a kvocientem -b a její součet je  . A platí
. A platí 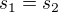
Obecně v úloze pro součty platí 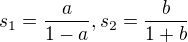 . Součty se rovnají, vyjádři b pomocí a.
. Součty se rovnají, vyjádři b pomocí a.
Až budeš mít předchozí úlohu vyřešenu, stačí za b dosadit 2a, vyřešit rovnici, získat a a to dosadit do vztahu pro součet.
Offline
#25 08. 05. 2016 15:50 — Editoval Akojeto (08. 05. 2016 16:04)
- Akojeto
- Příspěvky: 465
Re: Řešení Matematika+ 2016
Stačí dosadiť, vyjde len 1 priesečník [0;0].
Offline



