Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 11. 2016 08:03 — Editoval Slazer (04. 11. 2016 09:13)
Úplné systémy logických spojok
Mám zadefinovať sémantiku spojky  aby platilo, že
aby platilo, že  je úplný (plnohodnotný), ale
je úplný (plnohodnotný), ale 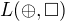 nie je. Predpokladať môžem len plnohodnotnosť
nie je. Predpokladať môžem len plnohodnotnosť 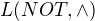 ,
,  a
a  .
.
Problém je, že neviem nájsť binárnu logickú spojku, ktorá spolu s  tvorí úplný systém. Píšem moje doterajšie úvahy.
tvorí úplný systém. Píšem moje doterajšie úvahy.
Ak by  bolo napríklad priamo
bolo napríklad priamo 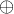 , tak zo spojok
, tak zo spojok 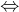 a
a 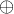 dokážem vytvoriť
dokážem vytvoriť  pomocou kontradikcie cez
pomocou kontradikcie cez 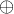 . Systém
. Systém 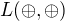 stále nebude plnohodnotný, ale
stále nebude plnohodnotný, ale 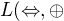 (teda
(teda  by zrejme mohol, ale neviem nájsť formulu vyjadrujúcu
by zrejme mohol, ale neviem nájsť formulu vyjadrujúcu 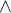 alebo
alebo  alebo
alebo 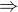 .
.
Ak by  nebolo
nebolo 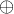 , tak mi zostáva posúdiť
, tak mi zostáva posúdiť  ďaľších spojok. Dve Shefferovské môžem vyradiť hneď, pretože
ďaľších spojok. Dve Shefferovské môžem vyradiť hneď, pretože 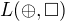 by bol plnohodnotný. Tiež môžeme vylúčiť
by bol plnohodnotný. Tiež môžeme vylúčiť  a
a 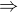 , lebo
, lebo  nebude úplný. Momentálne uvažujem nad T (tautológiou) a K (kontradikciou). Pomocou
nebude úplný. Momentálne uvažujem nad T (tautológiou) a K (kontradikciou). Pomocou 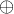 a T viem vytvoriť
a T viem vytvoriť 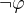 a preto aj
a preto aj 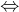 , čím by sa však
, čím by sa však 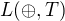 stal úplným (za podmienky, že
stal úplným (za podmienky, že 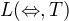 je úplný), čo je spor. Pomocou K viem vytvoriť
je úplný), čo je spor. Pomocou K viem vytvoriť  v
v 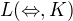 a tu som zatiaľ skončil.
a tu som zatiaľ skončil.
V systéme  ani
ani 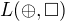 nesmie byť možné vytvoriť
nesmie byť možné vytvoriť 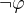 . Ak by to možné bolo, tak keďže
. Ak by to možné bolo, tak keďže 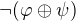 je ekvivalentné s
je ekvivalentné s 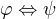 a
a  (teda vlastne
(teda vlastne  ) je úplný, tak aj
) je úplný, tak aj  by bol úplný, čo je spor.
by bol úplný, čo je spor.
Neúplné systémy: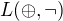
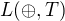
 (neviem vyjadriť
(neviem vyjadriť 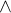 )
)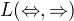
Úplné systémy: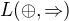

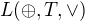
V úplnom systéme nemusí byť negácia (ako spojka).
Uvažujem nad úplnosťou:
(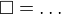 )
)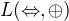
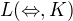
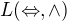
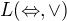
Sem som sa zatiaľ dostal. Ďakujem za pomoc.
Offline
- (téma jako nevyřešené označil(a) jelena)
#2 04. 11. 2016 11:44 — Editoval Sherlock (04. 11. 2016 11:54)
Re: Úplné systémy logických spojok
Dělám ten samej úkol ;)
Pokud je  neúplný, je neúplný i
neúplný, je neúplný i 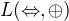 (negaci odpovídá
(negaci odpovídá 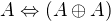 )
)
Podle mě sis správně všimnul, že 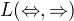 není úplný, ale
není úplný, ale 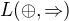 úplný je - zkus to nějak "obrátit", aby ti to vyšlo naopak.
úplný je - zkus to nějak "obrátit", aby ti to vyšlo naopak.
V úplnom systéme nemusí byť negácia (ako spojka).
Nemusí tam být přímo, musí ale být vyjádřitelná pomocí spojek, co v tom systému máš. :)
Offline
#3 04. 11. 2016 15:52 — Editoval Slazer (04. 11. 2016 15:55)
Re: Úplné systémy logických spojok
Hmm, zrejme som na to prišiel. Ešte rozmýšľam, ako dokázať, že 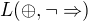 nie je úplný systém. Nejak ma to vedie k dôkazu, že nie je úplný pretože v
nie je úplný systém. Nejak ma to vedie k dôkazu, že nie je úplný pretože v 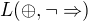 nemožno odvodiť tautológiu.
nemožno odvodiť tautológiu.
Ak by mal byť 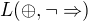 úplný, musí v ňom existovať formula pre negáciu. Predpokladám, že negáciu viem vytvoriť LEN ak viem vytvoriť tautológiu v systéme
úplný, musí v ňom existovať formula pre negáciu. Predpokladám, že negáciu viem vytvoriť LEN ak viem vytvoriť tautológiu v systéme 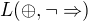 , ale neviem to dokázať.
, ale neviem to dokázať.
Viem, že sa to dá spraviť použiťím
a) 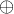 a
a 
b) 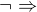 a
a 
ale ako dokázať, že bez tautológie nikdy nebude  ?
?
Offline
#4 05. 11. 2016 09:55 Příspěvek uživatele Sherlock byl skryt uživatelem byk7.
#5 05. 11. 2016 10:23 Příspěvek uživatele jelena byl skryt uživatelem byk7.
#6 07. 11. 2016 12:08
Re: Úplné systémy logických spojok
↑ Slazer: Ono to platí i naopak, přesněji "negaci umím vytvořit právě tehdy, když umím vytvořit tautologii". Důkaz je jednoduchý:
(i) 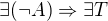 : pak
: pak 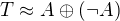
(ii)  : pak
: pak 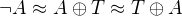 .
.
Hotovo. :)
Řekněme tedy, že máme v 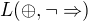 formuli
formuli  odpovídající negaci a předpokládejme navíc, že
odpovídající negaci a předpokládejme navíc, že 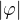 je minimální. Potom musí nastat jedna z možností
je minimální. Potom musí nastat jedna z možností 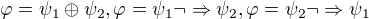 , kde
, kde  ,
,  a
a 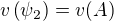 . Pak se ale snadno ukáže, že ani jedna z možností negaci neodpovídá. Spor. V
. Pak se ale snadno ukáže, že ani jedna z možností negaci neodpovídá. Spor. V 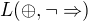 negaci nemáme.
negaci nemáme.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
