Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 01. 2017 22:01 — Editoval Al1 (24. 01. 2017 22:14)
Re: Druhá derivace
↑ Elisa:
Zdravím,
derivuješ podíl. Derivace čitatele (x-1) je rovna +1, nikoli (-1), takže hned první člen v čitateli zlomku je chybný.
A ještě: hned na počátku konstantu v součinu 1/2 nederivuješ ( dáváš ji do součinu s derivací funkce), ale pak s ní dál počítáš ve jmenovateli.
Offline
#7 25. 01. 2017 08:15
Re: Druhá derivace
Ahoj ↑ Elisa:,
Pozor, tiez treba pisat napr. f''(x) a nie f'' ako si napisala vyssie.
Lebo je jasne, ze si chcela vyjadrit hodnotu funkcie f'' v bode x.
Prakticky, ked vyjadris hodnotu funkcie bez |.|, tak casto v kritickych bodoch budes mat rozne hodnoty na lavo a na pravo ....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 25. 01. 2017 12:34 — Editoval vanok (25. 01. 2017 12:40)
Re: Druhá derivace
Pre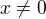 
mas 
. ... tak treba davat pozor ked 
Inac
Tvoja rovnost da 
... a z tym tiez sa mozes pobavit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 25. 01. 2017 13:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Druhá derivace
Zdravím,
už jste v debatě dost daleko, ale snad nebude na škodu, když doplním, že již hned na úvod ↑ Elisa: mohla použit úpravu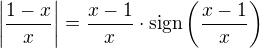 
, co nejvíce upravit původní zápis (nejlépe zjednodušit na součin) a až potom derivovat.
Jak již tu v tématu zaznělo, větší důraz, než samotné derivování, musí být nulovým bodům výrazu v absolutní hodnotě (rozbor jednostranných derivací a závěry o derivaci v těchto bodech). Ale to už bylo řečeno i od kolegů.
Offline
#12 28. 01. 2017 13:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Druhá derivace
↑ Elisa:
Zdravím,
pokud jsem nic nepřehlédla, tak bych měla stejný výsledek (po všech úpravách, jak máš). Úprava hned na úvod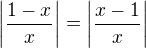 
se mi zdá přehlednější pro práci s nulovými body a znaménky na intervalech, potom pro využití derivace pro vyšetření funkce by se také více hodil zápis na konci předposledního řádku. Ale to jsou jen doporučení, nemají vliv na celkový výsledek.
"Funkce není spojitá" plyne již z def. oboru samotné funkce, jen můžeš došetřit typ bodu nespojitosti v x=0. Ze zápisu 1. derivace plyne, že derivace také neexistuje v bodě 
. Úlohou je vyšetření průběhu funkce, nebo něco jiného? Děkuji.
Offline
#14 30. 01. 2017 21:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Druhá derivace
↑ Elisa:
Zdravím, pokud bych potřebovala pro průběh funkce, tak bych spíš použila odstranění absolutní hodnoty na jednotlivých intervalech, zda se mi to přehlednější do tabulky a zejména pro vyšetření chování v nulových bodech absolutní hodnoty. Mít zápis co nejjednodušší a přehledný pro zamezení chybám z přepisu a nepozornosti.
Na druhou stranu - uvaž, že graf této funkce snadno nakreslíš bez podrobných kroků stanovených pro "průběh funkce". Vnitřní funkce je 
, tu nakreslíš a její absolutní hodnotu také. Kreslení odmocnin monotonních funkcí (na příslušných intervalech) bys také měla umět zvládnout, vyzkoušej, prosím.
Offline