Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 02. 2017 16:17
rovnováha bodu
Ahoj.
Zadání příkladu zní. Vypočtěte souřadnice bodu A(x,y) určující rovnovážnou polohu. Dáno m, h, k1,k2, l01, L02.
Chci se zeptat:
1) odkud se vzaly vzorce (1) (2)
2) proč se ve vzorcích na místo souřadnice x používá (x-h)
3) proč se x-h nepoužívá i ve vzorcích (1)
Moc děkuji za odpověď.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 07. 02. 2017 23:24
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnováha bodu
Zdravím,
pokud umístím počátek souřadnic do levého závěsu O (0, 0), potom souřadnice pravého závěsu jsou K(h, 0) a hledaného bodu A (x, y) - zde působí závaží. Z bodu A udělám kolmici na osu x, průsečík s osou označím X. Teď máme 2 pravoúhlé trojúhelníky: OXA (používáme pro výpočet úhlu  ) a AXK (pro úhel
) a AXK (pro úhel  ). Vzorce jsou z goniometrie pravoúhlého trojúhelníku (protilehlá/přepona, přilehlá/přepona), pro přeponu Pythagorova věta.
). Vzorce jsou z goniometrie pravoúhlého trojúhelníku (protilehlá/přepona, přilehlá/přepona), pro přeponu Pythagorova věta.
Stačí tak a je to již přehledné? Děkuji.
Offline
#3 08. 02. 2017 08:36 — Editoval aferon (08. 02. 2017 14:45)
Re: rovnováha bodu
↑ jelena:
Děkuji za odpověď. Míní se tedy tím zápisem (h-x) =x, x-ová souřadnice bodu A, kterou vyjadřujeme z trojúhelníku AXK vzhledem k počátku S.S ? Děkuji.
Edit: chci se ještě zeptat na síly v pružině S1 a S2? 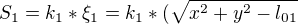
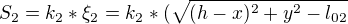
proč jsou takto jednotlivá prodloužení 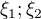 zapsána? Děkuji.
zapsána? Děkuji.
Offline
#4 08. 02. 2017 19:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnováha bodu
↑ aferon:
Zdravím a také děkuji.
(h-x) =x
toto není dobře, platilo by pouze, pokud je 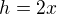 a bod A je přesně uprostřed celé délky mezi závěsy. Označení
a bod A je přesně uprostřed celé délky mezi závěsy. Označení  ,
,  je x-souřadnice našich bodů X, K, ale také tak můžeme označit velikost vzdálenosti těchto bodů od počátků (např. h (cm) a x (cm)). Obecně potřebujeme délku
je x-souřadnice našich bodů X, K, ale také tak můžeme označit velikost vzdálenosti těchto bodů od počátků (např. h (cm) a x (cm)). Obecně potřebujeme délku 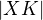 . bude přehlednější, když zapíšeš ve zvyklém označení pro vzdálenost
. bude přehlednější, když zapíšeš ve zvyklém označení pro vzdálenost 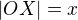 ,
,  , potom
, potom 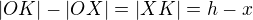 , délku strany
, délku strany 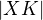 potřebujeme pro trojúhelník AXK, abychom určili velikost úhlu
potřebujeme pro trojúhelník AXK, abychom určili velikost úhlu  .
.
Prodloužení se počítá jako rozdíl mezi délkou po prodloužení a původní, tedy 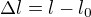 , původní délka
, původní délka 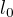 byla ze zadání, nová délka po prodloužení se počítá z trojúhelníků OXA a AXK (přepona trojúhelníku je délkou po prodloužení). Akorát je chybně umístěn znak odmocniny, má být tak:
byla ze zadání, nová délka po prodloužení se počítá z trojúhelníků OXA a AXK (přepona trojúhelníku je délkou po prodloužení). Akorát je chybně umístěn znak odmocniny, má být tak: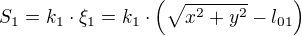 , kde
, kde . Obdobně opravit i pro 2. část:
. Obdobně opravit i pro 2. část: 
On ten obrázek je dost nepřehledný, zkus překreslit jen geometrii, bez vyznačení sil apod. a jen se podívat na rozměry pravoúhlých trojúhelníků. Bude to úplně jasné. Je tak? Děkuji.
Offline