Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 04. 2017 14:24
Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Zdravím.
Potřeboval bych pomoci s tímto problémem.
Kulička s hmotností m je umístěna na počátek dráhy  (například
(například 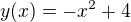 ). Počátek dráhy je v bodě
). Počátek dráhy je v bodě 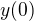 , počáteční rychlost kuličky je nulová a je uvedena do pohybu nekonečně malým impulsem. V jakém čase se dostane do bodu
, počáteční rychlost kuličky je nulová a je uvedena do pohybu nekonečně malým impulsem. V jakém čase se dostane do bodu 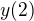 , zanedbáme-li tření, odpor vzduchu apod.
, zanedbáme-li tření, odpor vzduchu apod.
Zkoušel jsem na to jít přes zákon o zachování energie a spočítal si, velikost rychlosti v bodě 2. Dále jsem zkoušel určit okamžité zrychlení pomocí tíhového zrychlení a úhlu alfa, který okamžité zrychlení svírá s osou x, neboť alfa je funkcí 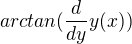 . Ale nikam jsem s tím nedošel.
. Ale nikam jsem s tím nedošel.
Děkuji.
Offline
#2 30. 04. 2017 17:57 — Editoval KennyMcCormick (17. 05. 2017 00:57)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
EDIT: Schoval jsem chybnou odpověď, přidávám doufejme správnou.
(Doufejme) správná odpověď:
Zjistíme poloměr oskulační kružnice:
1. derivace funkce je
 .
.2. derivace funkce je
 .
.V bodě
![kopírovat do textarea $[x,y]$](/mathtex/57/57a475f70048f0253c99bfacb0932ba4.gif) je poloměr kružnice
je poloměr kružnice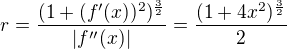 .
.Velikost rychlosti v bodě
![kopírovat do textarea $[x,y]$](/mathtex/57/57a475f70048f0253c99bfacb0932ba4.gif) je
je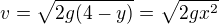 .
.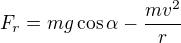
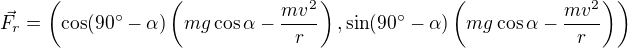 , tj.
, tj.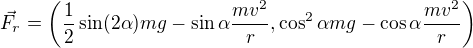
x-ová složka výslednice sil je
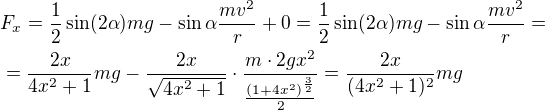 .
.x-ová složka zrychlení tedy je
 .
. Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#3 04. 05. 2017 16:23
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
↑ Hašiš:
Zadání úlohy je problematické, protože na velikosti "nekonečně malého" počátečního impulsu záleží, a to významně.
Do bodu 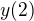 se kulička může dostat za libovolně dlouhou dobu, anebo také nikdy - právě podle velikosti impulsu, popřípadě podle velikosti počáteční výchylky. Lze akorát dostatečně přesně spočítat rychlost kuličky v daném bodě. Na to ale stačí energetická úvaha.
se kulička může dostat za libovolně dlouhou dobu, anebo také nikdy - právě podle velikosti impulsu, popřípadě podle velikosti počáteční výchylky. Lze akorát dostatečně přesně spočítat rychlost kuličky v daném bodě. Na to ale stačí energetická úvaha.
↑ KennyMcCormick:
Napadlo mě, že se odvození DR zkomplikuje tím, že  závisí také na rychlosti kuličky. Nebo se mýlím?
závisí také na rychlosti kuličky. Nebo se mýlím?
Offline
#4 04. 05. 2017 17:46
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Do bodu
se kulička může dostat za libovolně dlouhou dobu, anebo také nikdy
Takže kdybych začínal z koncové polohy a vyslal kuličku nahoru se správnou rychlostí, zastaví se v rovnovážné poloze po nekonečném čase, je to tak?
Napadlo mě, že se odvození DR zkomplikuje tím, že
závisí také na rychlosti kuličky.
Kvůli dostředivé síle?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#5 04. 05. 2017 18:07
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
↑ KennyMcCormick:
Ano.
Ano.
Před pěti lety zde byla podobná úloha. Jednalo se o matematické kyvadlo začínající pohyb v horní poloze.
http://forum.matweb.cz/viewtopic.ph … 75#p297975
Řešení je na konci tématu, zde to bude v aproximaci asi podobné, zejména výpočet pro dlouhé doby, kdy většina času uběhne, než se ta kulička vůbec trochu vzdálí od rovnovážné polohy.
Offline
#6 04. 05. 2017 20:38
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Bude složka tíhové síly, která se podílí na vzniku  , součástí dostředivé síly?
, součástí dostředivé síly?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#7 05. 05. 2017 05:00
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
↑ KennyMcCormick:
Tomu moc nerozumím, jak to myslíš. Zda bude ve vyjádření  figurovat
figurovat  ?
?
Já bych to celé počítal tak, že nejdřív bych z energetické bilance odvodil 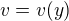 , tj. závislost absolutní hodnoty rychlosti na svislé souřadnici. Za další bych odvodil
, tj. závislost absolutní hodnoty rychlosti na svislé souřadnici. Za další bych odvodil  , tj. závislost délky trajektorie na svislé souřadnici (spočítat délku křivky integrálem). Pak lze z
, tj. závislost délky trajektorie na svislé souřadnici (spočítat délku křivky integrálem). Pak lze z  a
a 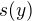 snadno vyloučit
snadno vyloučit  a dostaneme dif. rovnici, která již nebude moc hezká.
a dostaneme dif. rovnici, která již nebude moc hezká.
I v tomto případě ale lze provést aproximaci pro malé vzdálenosti od rovnovážné polohy. Délku 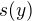 oblouku paraboly lze v okolí vrcholu dobře aproximovat délkou jeho průmětu na osu
oblouku paraboly lze v okolí vrcholu dobře aproximovat délkou jeho průmětu na osu  . Tím se to celé náramně zjednoduší a mělo by vyjít něco jako
. Tím se to celé náramně zjednoduší a mělo by vyjít něco jako ,
, .
.
Zde už je mimochodem vidět, že počáteční podmínka nemůže být nulová, pokud chceme dostat netriviální řešení. Anebo jinak, ke každému libovolnému času  lze najít takovou počáteční podmínku, aby kulička v tomto čase nesjela až dolů.
lze najít takovou počáteční podmínku, aby kulička v tomto čase nesjela až dolů.
Offline
#8 05. 05. 2017 20:36 — Editoval KennyMcCormick (06. 05. 2017 01:29)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Tomu moc nerozumím, jak to myslíš. Zda bude ve vyjádření
figurovat
?
Myslel jsem to tak, jestli bude normálová složka tíhové síly součástí dostředivé síly, tj. jestli .
.
Děkuju za rady k řešení, zítra se na to podívám. :)
Z čeho v tomhle případě pochází, na mikroskopické úrovni, ta dostředivá síla?
EDIT: Otázky v tomhle komentáři můžeš ignorovat, myslím, že je mi to už jasné.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#9 05. 05. 2017 21:45 — Editoval KennyMcCormick (06. 05. 2017 00:39) Příspěvek uživatele KennyMcCormick byl skryt uživatelem KennyMcCormick. Důvod: Omyl...
#10 06. 05. 2017 01:21 — Editoval KennyMcCormick (10. 05. 2017 03:45)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Pokud bych měl kopec ve tvaru paraboly (a ne např. rouru ve tvaru paraboly, která by vynucovala dráhu kuličky přesně dráhu ve tvaru paraboly), kulička by odletěla od paraboly v kladném směru osy x v okamžiku, kdy by o̶d̶s̶t̶ř̶e̶d̶i̶v̶á̶ ̶s̶í̶l̶a̶ ̶u̶ž̶ ̶n̶e̶b̶y̶l̶a̶ ̶d̶o̶s̶t̶a̶t̶e̶č̶n̶ě̶ ̶k̶o̶m̶p̶e̶n̶z̶o̶v̶a̶n̶á̶ ̶n̶o̶r̶m̶á̶l̶o̶v̶o̶u̶ ̶s̶l̶o̶ž̶k̶o̶u̶ ̶t̶í̶h̶o̶v̶é̶ ̶s̶í̶l̶y̶ normálová složka tíhové síly už nebyla větší nebo rovna dostředivé síle.
Je to tak?
EDIT: "odstředivá síla" -> "reakce paraboly na sílu 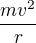 "
"
EDIT: "reakce paraboly na sílu 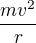 " -> "normálová složka tíhové síly už nebyla větší nebo rovna dostředivé síle"
" -> "normálová složka tíhové síly už nebyla větší nebo rovna dostředivé síle"
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#11 06. 05. 2017 05:58
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
K příspěvku #10.
Zajímavá otázka. Bylo by užitečné pokusit se o nějakou analýzu. Asi záleží na počátečních podmínkách. Domnívám se, že pokud bychom kuličku na začátku příliš neurychlili, nikdy by se od parabolického kopce neodlepila. V průběhu sjíždění by tlak na dráhu asymptoticky klesal k nule. Později by kulička v podstatě volně padala podél paraboly. To je ovšem jen můj první pohled na věc, mohu se mýlit.
Offline
#12 06. 05. 2017 07:56
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
K dostředivé síle.
Prošel jsem tvé dřívější zápisy. Nesedí mi tam, že  nejdřív uvádíš jako "sílu, kterou parabola působí na kuličku", zatímco později je
nejdřív uvádíš jako "sílu, kterou parabola působí na kuličku", zatímco později je 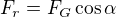 , což je normálová složka tíhové síly.
, což je normálová složka tíhové síly.  jsi dále využíval k výpočtu, proto z toho vyplynula moje obava o komplikaci řešení díky chybějící dostředivé síle.
jsi dále využíval k výpočtu, proto z toho vyplynula moje obava o komplikaci řešení díky chybějící dostředivé síle.
Řekl bych, že to má být takto: ,
,
(reakce dokonale kluzké podložky je samozřejmě také normálová).
Ale normálové síly nás nemusí zajímat (pokud není dána možnost odlepení kuličky od paraboly). Je tedy třeba vzít tečnou složku tíhové síly  , a tu pak rozložit na vodorovnou a svislou komponentu.
, a tu pak rozložit na vodorovnou a svislou komponentu.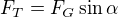 =>
=> 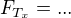
Takto dojdeme ke stejnému vyjádření 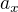 , jak jsi odvodil ty:
, jak jsi odvodil ty: .
.
Co tomu říkáš?
:-)
Offline
#13 06. 05. 2017 20:57 — Editoval KennyMcCormick (10. 05. 2017 03:46)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Díky. :) Předtím, než budu psát něco dalšího: Souhlasíš, že můj výsledek (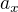 ) je správně, ale můj postup by měl být jiný. Chápu tě správně?
) je správně, ale můj postup by měl být jiný. Chápu tě správně?
EDIT: K tomu si navíc myslím, že jsem tady: ↑ KennyMcCormick: použil termín "odstředivá síla" v chybném významu - měl jsem napsat "reakce paraboly na sílu 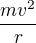 ". Opravím to.
". Opravím to.
EDIT: Ne, měl jsem tam napsat "normálová složka tíhové síly už nebyla větší nebo rovna dostředivé síle". Znovu opraveno...
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#14 08. 05. 2017 22:28
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
↑ KennyMcCormick:
Ano, tak jsem to myslel. Ale to "ax" nam vyslo stejne a snad spravne :)
Na terminologii odstrediva/dostrediva nejsem haklivy, hlavne kdyz se vi, o co jde.
Mel jsem (jeste mam) omezene spojeni, zitra to bude lepsi.
Offline
#15 10. 05. 2017 04:04 — Editoval KennyMcCormick (10. 05. 2017 04:20)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Díky za odpovědi. :) Takže v mém prvním komentáři je potřeba provést 2 změny:
1.  není
není  , kde
, kde 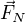 je normálová složka tíhové síly, ale platí
je normálová složka tíhové síly, ale platí
2. Síla, která způsobuje pohyb koule v tečném směru, není výslednice sil, ale tečná složka výslednice sil.
Je to tak?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#16 10. 05. 2017 23:49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Souhlasím. Jen bych ve druhém tvrzení místo "pohyb" použil raději "zrychlení", ale určitě jsi to myslel správně.
Přidávám obrázek pro přehlednost:
 - tíhová síla
- tíhová síla - tangenciální komponenta síly (způsobující změny velikosti rychlosti hmot. bodu
- tangenciální komponenta síly (způsobující změny velikosti rychlosti hmot. bodu - normálová komponenta tíhové síly
- normálová komponenta tíhové síly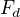 - dostředivá síla (způsobující změny směru pohybu hmot. bodu)
- dostředivá síla (způsobující změny směru pohybu hmot. bodu)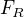 - síla reakce podložky (neboli tlak paraboly na hmotný bod)
- síla reakce podložky (neboli tlak paraboly na hmotný bod) - celková síla určující pohyb hmot. bodu
- celková síla určující pohyb hmot. bodu
Platí: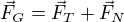 , tj. rozklad tíhové síly do komponent N a T
, tj. rozklad tíhové síly do komponent N a T , tj, pokud Fd=Fn, bude tlak na podložku nulový
, tj, pokud Fd=Fn, bude tlak na podložku nulový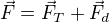 , tj. rozklad výsledné síly na komponenty určující velikost a směr rychlosti
, tj. rozklad výsledné síly na komponenty určující velikost a směr rychlosti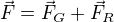 , to jsou jediné dvě "originální" síly působící na hmotný bod, které určují jeho pohyb
, to jsou jediné dvě "originální" síly působící na hmotný bod, které určují jeho pohyb
Obrázek je vždy užitečný :)
Například teď už si nemyslím, že máme správně vypočteno to 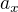 , protože
, protože 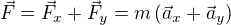 .
.
Postup naznačený v příspěvku #7 by ovšem měl být ok.
Offline
#17 11. 05. 2017 20:01 — Editoval KennyMcCormick (11. 05. 2017 20:42)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Jen bych ve druhém tvrzení místo "pohyb" použil raději "zrychlení", ale určitě jsi to myslel správně.
Ano, tak jsem to myslel. :)
Takže v případě, že se těleso pohybuje po zakřivené dráze, rovnice
není
, protože výslednice sil nemíří v tečném směru.
Je to tak?
EDIT: Tzn. stačí jediná úprava v mém prvním příspěvku:
1.
není
, kde
je normálová složka tíhové síly, ale platí
.
(+ přepočítat zbytek výpočtu)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#18 11. 05. 2017 20:55
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
↑ KennyMcCormick:
Ano, výslednice míří poněkud jinam, víc ke středu křivosti dráhy.
Udělal jsem výpočet přes délku křivky (paraboly). Až si najdu čas, dám ho sem. O přepočet 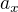 jsem se zatím nesnažil.
jsem se zatím nesnažil.
Offline
#19 11. 05. 2017 21:45
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
OK... to můžu přepočítat já, jenom jsem se chtěl ujistit, že to přepočítávám správným způsobem, než začnu.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#20 14. 05. 2017 07:51 — Editoval KennyMcCormick (17. 05. 2017 00:58)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Nerovnoměrně zrychlený křivočarý pohyb - výpočet času v bodě
Zjistíme poloměr oskulační kružnice:
1. derivace funkce je .
.
2. derivace funkce je .
.
V bodě ![kopírovat do textarea $[x,y]$](/mathtex/57/57a475f70048f0253c99bfacb0932ba4.gif) je poloměr kružnice
je poloměr kružnice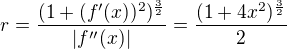 .
.
Velikost rychlosti v bodě ![kopírovat do textarea $[x,y]$](/mathtex/57/57a475f70048f0253c99bfacb0932ba4.gif) je
je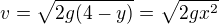 .
.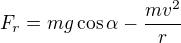
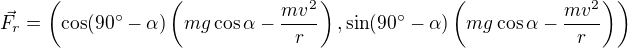 , tj.
, tj.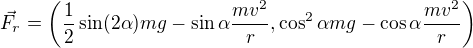
x-ová složka výslednice sil je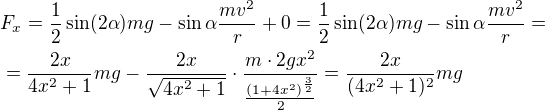 .
.
x-ová složka zrychlení tedy je .
.
To by už mohlo být správně? :)
EDIT: Přidal jsem tuhle odpověď do svého prvního příspěvku.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline

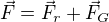 , kde
, kde 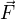 je výsledná síla působící na kuličku,
je výsledná síla působící na kuličku, 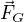 je tíhová síla.
je tíhová síla. .
.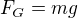
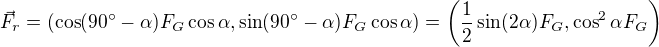
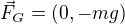
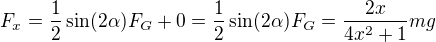 .
.