Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 06. 2018 16:09 — Editoval KennyMcCormick (01. 08. 2018 10:47)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohybová rovnice
Nejdřív zjisti, za jaký čas vyteče všechna voda.
Za jaký čas vyteče voda?
Vagón musí ztratit hmotnost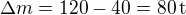 .
.
Tuto hmotnost ztratí za čas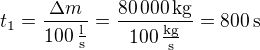 .
.
Takže vidíme, že vagón za 10 minut neztratí všechnu vodu.
Skrytá část je špatně, protože samozřejmě  jenom pro konstantní hmotnost. Sorry.
jenom pro konstantní hmotnost. Sorry.
Edit: Teď si myslím, že jsem to původně napsal správně. Přečti si můj komentář tady (↑ KennyMcCormick:) pro vysvětlení a potom pokračuj ve skryté části.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#4 17. 06. 2018 19:46
Re: Pohybová rovnice
↑ StandaA:↑ KennyMcCormick:
Mám pro vás dvě zprávy, obě špatné.
1. Navržený postup je špatně.
Vztah 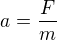 platí POUZE, když je hmotnost konstantní, což zde evidentně neplatí.
platí POUZE, když je hmotnost konstantní, což zde evidentně neplatí.
a z toho plyne, že
2. Uvedený výsledek je taktéž špatně.
Budeš muset použít obecnější vztah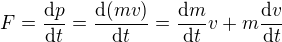
a pokud tedy 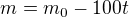 , dostaneme
, dostaneme 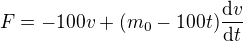
a separací proměnných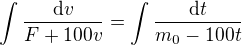
zbytek jsou počty
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 17. 06. 2018 20:12
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohybová rovnice
No jo, samozřejmě.
A to jsem se ještě radoval, jak mi to hezky vyšlo...
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#6 14. 07. 2018 23:34
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohybová rovnice
↑ zdenek1:
Není to jinak?
https://en.wikipedia.org/wiki/Variable- … _accretion
Potom by jeho řešení a výsledek byly správně, protože by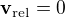 .
.
(Plus, tady je napsáno, že 2. Newtonův zákon je možné aplikovat jen na celý systém jako takový (tj. i na vodu).)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#7 15. 07. 2018 11:23 — Editoval MichalAld (15. 07. 2018 12:12)
Re: Pohybová rovnice
Já teď nemám čas to řešit, ale nejsem si úplně jistý - ta vytékající voda možná odnáší část hybnosti a tu bychom do toho možná měli nějak zakomponovat.
Jinak by to totiž podle mě mělo jít i bez komplikovaných složených derivací, protože když F=dp/dt, a F je konstantní, tak bychom prostě mohli říct, že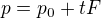
no a ze vztahu p=mv spočítat tu rychlost.
Jenže to je určitě špatně, protože kdyby byla síla nulová, tak by se hybnost zachovávala, a z toho by plynulo, že rychlost bude narůstat s tím, jak vytéká voda.
To je ale určitě nesprávně. Vytékající voda nám vagón urychlovat nebude, což je celkem zřejmé, když si to představíme v opuštěném kusu vesmíru (a né na Zemi) - vytékající voda se prostě bude pohybovat vpřed stejnou rychlostí jako když byla v té cisterně. Nemůže to být jinak, protože v soustavě která se bude pohybovat stejně rychle jako cisterna uvidíme prostě jen proud vody kolmo na cisternu, a jinak se tam nic nepohybuje. Proud vody se nebude pohybovat směrem "dozadu".
Takže to co navrhuje ↑ KennyMcCormick: je zřejmě správný přístup.
Takže ono to vlastně ukazuje, že ten původní postup je správný, né ?
Protože ve vztahu 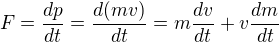
tedy spíše takto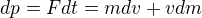
se ten druhý člen obsahující dm nevyužije ke zvýšení hybnosti vagónu s cisternou, ale prostě se zahodí (voda poletí dál vedle cisterny, aspoň v prázdném vesmíru by letěla).
(úžasné, jak se takové jednoduché věci dokáží krásně zamotat)
Offline
#8 15. 07. 2018 12:38
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohybová rovnice
↑ MichalAld:
Z těch dvou odkazů ze svého minulého příspěvku bych řekl, že:
1.
Jinak by to totiž podle mě mělo jít i bez komplikovaných složených derivací, protože když F=dp/dt, a F je konstantní, tak bychom prostě mohli říct, že
no a ze vztahu p=mv spočítat tu rychlost.
Jenže to je určitě špatně, protože kdyby byla síla nulová, tak by se hybnost zachovávala, a z toho by plynulo, že rychlost bude narůstat s tím, jak vytéká voda.
 je hybnost systému vagón+voda. Tj. v případě nulové síly by se
je hybnost systému vagón+voda. Tj. v případě nulové síly by se  mělo zachovávat.
mělo zachovávat.
2.
Nemůžeme psát
pro systém s proměnnou hmotností (v klasické mechanice).
Nejdřív si musíme vyjádřit 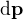 (změnu hybnosti celého systému) tak, jako to dělají v prvním odkazu a dosadit ji do 2. Newtonova zákona.
(změnu hybnosti celého systému) tak, jako to dělají v prvním odkazu a dosadit ji do 2. Newtonova zákona.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#9 15. 07. 2018 15:35
Re: Pohybová rovnice
KennyMcCormick napsal(a):
↑ MichalAld:
Z těch dvou odkazů ze svého minulého příspěvku bych řekl, že:
1.Jinak by to totiž podle mě mělo jít i bez komplikovaných složených derivací, protože když F=dp/dt, a F je konstantní, tak bychom prostě mohli říct, že
no a ze vztahu p=mv spočítat tu rychlost.
Jenže to je určitě špatně, protože kdyby byla síla nulová, tak by se hybnost zachovávala, a z toho by plynulo, že rychlost bude narůstat s tím, jak vytéká voda.
je hybnost systému vagón+voda. Tj. v případě nulové síly by se
mělo zachovávat.
Jo, to je jisté, celková hybnost se musí zachovávat, a to zahrnuje i tu hybnost vody, co vytekla.
To samé, když bude nenulová síla - přírustek hybnosti dp = F dt bude zahrnovat přírustek hybnosti celého systému, tedy cisterny a k tomu i vody, co vytekla. O tu se nám zase sníži hybnost samotné cisterny.
Offline
#10 16. 07. 2018 01:02
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohybová rovnice
To samé, když bude nenulová síla - přírustek hybnosti dp = F dt bude zahrnovat přírustek hybnosti celého systému, tedy cisterny a k tomu i vody, co vytekla. O tu se nám zase sníži hybnost samotné cisterny.
Jestli to myslíš tak, že se o hybnost vody sníží hybnost cisterny, tak to platí jenom pro nulovou sílu, je to tak?
Jestli myslíš, že se o zvýšení hybnosti celého systému sníží hybnost cisterny, tak zvýšení hybnosti celého systému je podle mě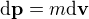 , zatímco zvýšení hybnosti cisterny je podle mě
, zatímco zvýšení hybnosti cisterny je podle mě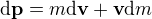 .
.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#11 16. 07. 2018 15:43
Re: Pohybová rovnice
Já vážně nevím, jak přesně by to mělo být. Ale poslední pokus, co mě napadl, dává aspoň limitní výsledky správně. Takže:
Pro hybnost cisterny by mělo platit: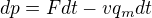
qm - je hmotnostní průtok vytékající kapaliny (kg/s),
v - není výtoková rychlost ale rychlost pohybu té cisterny
takže v*qm*dt je element hybnosti, jež "vyteče" spolu s vodou
a F*dt je element hybnosti, jež cisterna získá od vnější síly
Nevím, jestli je to správně, ale přijde mi to docela logické.
Dále už je to jen matematika. Nejprve to napíšeme v "matematicky korektním" tvaru, tedy: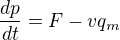
dosadíme za p = mv
No ta teď - ten člen dm/dt je přesně to co máme na druhé straně jako -qm. Takže když to tam dosadíme, dostaneme
Když to máme na obou stranách rovnice, tak to můžeme zrušit, čímž dostaneme klasické
až na to, že m je funkcí času, není to konstanta, 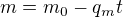
Nevím jestli je ten vzorec správný, pro nulovou sílu ovšem správný je (že rychlost se zachovává).
Pokud nás nezajímá rychlost, ale hybnost, použijeme ten první vztah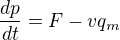
Ten je pro nulovou sílu také správný - hybnost klesá lineárně v čase. Díky tomu, že lineárně klesá hmotnost. Takže rychlost se nebude měnit.
Jestli je to ale opravdu správně, to já vážně nevím. Ale připadá mi to tak.
Offline
#12 17. 07. 2018 03:36 — Editoval KennyMcCormick (01. 08. 2018 10:48)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohybová rovnice
Takhle to počítat podle mě půjde, ale pak už nebude platit, že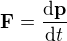 , tak nevím, jak se na to bude dívat jeho učitel...
, tak nevím, jak se na to bude dívat jeho učitel...
Podle dvou odkazů, které jsem dal tady (↑ KennyMcCormick:), je síla změna hybnosti za čas celého systému s konstantní hmotností, tj. změna hybnosti v 2. Newtonově zákonu není změna hybnosti cisterny, ale změna hybnosti systému cisterna + voda.
Já bych použil vzorec z https://en.wikipedia.org/wiki/Variable- … n/ejection, odvozený z 2. Newtonova zákona: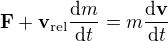 , kde
, kde 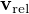 je relativní rychlost vody vůči cisterně.
je relativní rychlost vody vůči cisterně.
Protože voda tryská kolmo, nebude mít na situaci žádný vliv, takže druhý člen odstraníme a získáme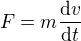 , což dá výsledek, ke kterému měl dojít ↑ StandaA:.
, což dá výsledek, ke kterému měl dojít ↑ StandaA:.
(Je to totéž jako to, co píšeš ty, ale možná se standardnějším významem pro 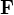 ...)
...)
Edit: Pokud nikdo nemá žádné námitky, označím téma znovu za vyřešené. 🙂
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline

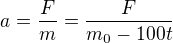 .
.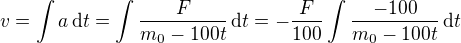 .
.