Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 20. 12. 2018 20:43
Re: Limita
↑ Pomeranc:
A ako urcim ci ma zmysel? Mam si limitu rozdelit na 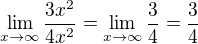 a
a 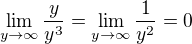
a teda 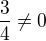 cize nema zmysel?
cize nema zmysel?
Offline
#4 21. 12. 2018 00:15
Re: Limita
↑ az:
Toto není správný postup. Je to chyba, výraz, který chceš zlimitit je zlomek s polynomy.
Nenech se zmást těmi více proměnnými a pracuj se zlomkem korektně, jak jste se to učili.
Vezmeš si přímky procházející počátkem. Mohou to být např. y=x, y=-x, y=0 atd.
(Resp. k danému místu se budeš blížit z různých směrů.)
Spočítáš limity. Co musí být splněno, aby limita existovala?
Offline
#5 21. 12. 2018 11:09 — Editoval Rumburak (21. 12. 2018 13:14)
Re: Limita
↑ az:
Ahoj. Domnívám se, že by též pomohla transformace do polárních souřadnic:
 ,
,  .
.
Tím dojdeme k jakési funkci ![kopírovat do textarea $[r, t] \mapsto g(r, t)$](/mathtex/36/3612c0663fb4ba6570cc9619ea7a5284.gif) a zkoumáme pak existenci limity
a zkoumáme pak existenci limity
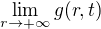
v závislosti na paremetru  a případnou stejnoměrnost této limity vzhledem k parametru
a případnou stejnoměrnost této limity vzhledem k parametru  .
.
(V podstatě jde o podrobnější náčrt myšlenky z příspěvku kolegy ↑ Pomeranc: .)
Offline
#6 21. 12. 2018 12:32
Re: Limita
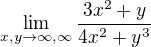
Co bych zkusil já - nejprve dokázat, že limita neexistuje. Tj že výsledek závisí na křivce, po které se do cílového bodu dostaneme.
Zkusíme třeba jednoduchou křivku y = x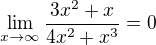
Další pokus může být třeba x = y^3
To by mělo stačit jako důkaz, že limita neexistuje. Nebo né ?
Offline
#7 21. 12. 2018 16:19
#8 22. 12. 2018 15:36
Re: Limita
↑ Pomeranc:
Mate na mysli postup co spravil MichalAld? No limita ma zmysel ak sa limita plusova a limita minusova rovanju a v pripade ked ide limita do nekonecna tak existuje, ak nie je obmedzeny definicny obor a funkcia nie je periodicka. Ospravedlnujem sa ak to vravim chybne, ale na strednej toto ucivo uz nepreberame, studujem si to sam.
↑ Rumburak:
Vas postup je podrobnejsi nacrt myslienky od Pomeranca? Myslel som si ze podrobnejsi nacrt myslienky od Pomeranca spravil MichalAld.
Offline
#9 22. 12. 2018 16:23
Re: Limita
↑ az: Co je to plusova a minusova limita? Ten prvy odstavec znie ako by islo o funkciu jednej premennej. Navyse to s limitou v nekonecne ani nie je pravda, napriklad 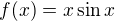 je definovana na celom
je definovana na celom  , nie je periodicka, ale limitu v nekonecne nema.
, nie je periodicka, ale limitu v nekonecne nema.
Offline
#10 23. 12. 2018 00:26
Re: Limita
↑ az:
S limitou funkce 2. proměnných je to složitější než u jedné proměnné. Zatímco u jedné proměnné se to k tomu bodu, kde limitu stanovujeme může "blížit" jen zleva a zprava, u limity dvou (a více) proměnných se to k němu může blížit z nekonečného množství směrů. A "směr" vlastně není ten správný pojem. Lepší by bylo říci nekonečně mnoha způsoby.
Pokud si dobře vzpomínám, tak nelze obecně dokázat, že taková limita existuje. Můžeme zkusit dokázat, že neexistuje - jako v tomto případě, můžeme zkusit zavést polární souřadnice, a pokud výsledek nezávisí na  , máme vyhráno a limita existuje - a pokud se nepodaří ani jedno, tak prostě nevíme. Možná existují ještě nějaké další triky, jak zjistit, zda limita existuje nebo né, ale obecně to myslím nejde.
, máme vyhráno a limita existuje - a pokud se nepodaří ani jedno, tak prostě nevíme. Možná existují ještě nějaké další triky, jak zjistit, zda limita existuje nebo né, ale obecně to myslím nejde.
Offline
#12 24. 12. 2018 12:33
Re: Limita
Ahoj ↑ MichalAld:,
Presnejsie mozes povedat, ze je pochopitelne vzdy mozne pouzit definiciu limity.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 25. 12. 2018 18:24
Re: Limita
↑ MichalAld:
Dakujem za objasnenie. Co som pozeral ja tak existuju dva primarne sposoby overenia existencie, jeden je pomocou priamok, co ste robili vy. A druhy je pomocou viacnasobnych (opakovanych) limit.
kaja.marik napsal(a):
dvojna limita je limita funkce dvou promennych, takze zhruba receno, pri vypoctu limity v bode (0,0) se k tomuto blodu blizime soucasne ze vsech stran a po vsech moznych cestach. Je to opravdu dost vulgarne a nepresne receno, je to proste limita funkce dvou promennych tak jak je definovana pomoci okoli nebo epsilon a delta.
dvojnasobna limita: k tomu bodu (0,0) se blizime tak, ze nejdriv stahneme k nule jednu promennou a potom drunou. pocitaji se tedy dve limity funkce jedne promenne a znamena to ze se k bodu blizime po ose x nebo po ose y.
pokud neexistuje dvojnasobna limita nebo pokud ty dvojnasobne limity nejsou stejne, tak dvojna limita neexistuje.
pokud jsou obe dvojnasobne limity stejne, pak to pro dvojnou limitu vubec ni neznamena.
----------------------------------------------------------------
„Táák,“ vzdychl Kája zklamaně. „To jsou vymejšlenosti na tom světě!“
Offline
#14 25. 12. 2018 18:31
Re: Limita
Ahoj ↑ az:,
Vies ako sa definuje limita funkcie f dvoch premennych v bode (a,b)?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 25. 12. 2018 19:26 — Editoval misaH (25. 12. 2018 19:28)
- misaH
- Příspěvky: 13433
Re: Limita
Z googlu:
Zdá sa, že táto problematika je náročnejšia než by sa amatérovi mohlo zdať...
Offline
#16 27. 12. 2018 11:02
Re: Limita
↑ az:
Zdravím.
Neřekl bych, že mnou navržený postup je podrobněji rozepsaný postup jmenovaného kolegy,
o něco takového jsem se ani nesnažil. Jde spíše o konkretisaci onoho postupu. Přechodem
k polárním souřadnicím  je totiž ihned vidět, že limita pro
je totiž ihned vidět, že limita pro  závisí na
závisí na  , což je
, což je
pro uvedenou úlohu skutečností klíčového významu.
Offline
#17 27. 12. 2018 12:18 — Editoval vanok (27. 12. 2018 12:19)
Re: Limita
Pozdravujem ↑ Rumburak:,
Skutocny problem je, ze tato tema sa da skutocne pracovat napr. v normovanych priestoroch ( tu v konecneho rozmeru, a netreba zabudnut ze vtedy su vsetki normy ekvivalentne). No vsak to nie je stredoskolakom pristupne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 27. 12. 2018 22:48
Re: Limita
az napsal(a):
↑ MichalAld:
Dakujem za objasnenie. Co som pozeral ja tak existuju dva primarne sposoby overenia existencie, jeden je pomocou priamok, co ste robili vy. A druhy je pomocou viacnasobnych (opakovanych) limit.
Jenže všechny tyhle způsoby slouží jen k důkazu toho, že limita neexistuje. Takže pokud si zvolíme křivku y=kx a výsledek nějak závisí na k, tak limita neexistuje. Pokud výsledek na k nezávisí, nic to neznamená.
Existuje nekonečné množství křivek typu y=f(x) (případně parametricky popsaných tj x = x(t) a y = y(t)), které bychom museli prověřit, abychom prokázali, že limita skutečně existuje. Ve škole jsme měli příklady, které na spoustu křivek reagovaly "dobře" - tj dávaly pořád stejný výsledek. Ale stejně existovala křivka, pro kterou daly výsledek jiný.
Jediný způsob co znám, jak dokázat existenci takové limity je použít polární souřadnice - a když výsledek nezávisí na phi, tak limita existuje.
Ale je možné, že eixistují ještě nějaké jiné hacky, jak existenci limity dokázat. Já je ale neznám.
Offline
#19 28. 12. 2018 09:36
Re: Limita
Cau ↑ MichalAld:,
Vyssie som napisal co treba na to.
No tu ti dam jednoduchy priklad kde dokazem existenciu limity inac ako pises.
Priklad.
Dokazte, ze 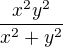 ma limitu v bode
ma limitu v bode 
Na dokaz, staci: Vieme, ze 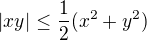 pre lubovolne realne cisla x,y.
pre lubovolne realne cisla x,y.
Tak plati,  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

![kopírovat do textarea $\lim_{[x,y]\to[0,0]} \frac{x^{5}}{xy^{2}+(\sqrt{y})^{5}}.$](/mathtex/bd/bd23a163f88a5aad9b313bf26f6e98c6.gif)
 za
za  a
a  určíme typ limity "nula lomené nula". Uvedenú limitu budeme riešiť substitúciou. Za vhodnú považujeme kvadratickú substitúcia, ktorá z geometrického hľadiska predstavuje približovanie sa k bodu
určíme typ limity "nula lomené nula". Uvedenú limitu budeme riešiť substitúciou. Za vhodnú považujeme kvadratickú substitúcia, ktorá z geometrického hľadiska predstavuje približovanie sa k bodu ![kopírovat do textarea $[x,y]=[0,0]$](/mathtex/ba/ba2776c988d599c86f52fb8de771643d.gif) po krivkách:
po krivkách:![kopírovat do textarea $\lim_{[x,y]\to[0,0]} \frac{x^{5}}{xy^{2}+(\sqrt{y})^{5}}=\left|Subst. \ x=t, y=k\cdot t^{2}; t\to 0, k\in\mathbb{R}\right|= $](/mathtex/43/43c23fbd3c8a874a66957b1ae17625c7.gif)


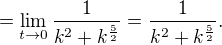
 (t.j., napríklad pre
(t.j., napríklad pre 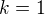 má hodnotu
má hodnotu  , kým pre
, kým pre 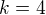 má hodnotu
má hodnotu 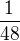 ),
), ![kopírovat do textarea $\lim_{[x,y]\to[0,0]} \frac{x^{5}}{xy^{2}+(\sqrt{y})^{5}}$](/mathtex/14/14b0a47fa41f4464d6b68b9363fc4dbd.gif) neexistuje.
neexistuje.