Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 25. 02. 2019 22:00 — Editoval Blyat (25. 02. 2019 22:01)
Re: POMOC (rovnice hyperboly)
↑ Al1:
omlouvám se male dnes byla první hodina kdy jsem na látku byl, předtím jsem týden chyběl.. a dostal jsem za povinnost toto na zítra mít, tudíž nevím jak se počítají zmíňěné poloosy.. jsou to hodnoty a,b ve středové rovnici?
Offline

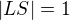 a vedlejší poloosu vypočítáš právě z tebou uvedeného vztahu (ale opravím ho):
a vedlejší poloosu vypočítáš právě z tebou uvedeného vztahu (ale opravím ho):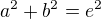
![kopírovat do textarea $\frac{(y-n)^{2}}{a^{2}}-\frac{(x-m)^{2}}{b^{2}}=1, S[m,n]$](/mathtex/96/9648787f73d2af94bc3ed26a2a4b95a0.gif)