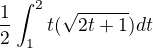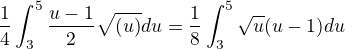Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » krivkovy integral - parabola (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 01. 2021 17:30
krivkovy integral - parabola
 ,C je cast paraboly
,C je cast paraboly 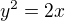 ,
, 
c(t)=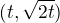
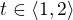
 ,
, a
a  ,
,
c´(t)=
||c´(t)||=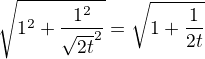
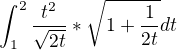
vysledok: ![kopírovat do textarea $[\frac{5}{6}\sqrt{5}-\frac{1}{5}\sqrt{3}]$](/mathtex/22/2248e94ebab3db39c2ff9ecd90ee7926.gif)
Chcem sa spytat ci je dobra parametrizacia lebo sa neviem dopracovat k vysledku. Dakujem za kazdu radu, pomoc.
Offline
- (téma jako vyřešené označil(a) MarST)
#6 14. 01. 2021 19:44 — Editoval laszky (14. 01. 2021 19:47)
Re: krivkovy integral - parabola
↑ MarST:
A dovedl bys vyjadrit [mathjax]t[/mathjax] z rovnice [mathjax]u=1+2t[/mathjax]? Navic neni substituce spravne provedena, za [mathjax]\mathrm{d}t[/mathjax] neni dosazeno (ono tam to [mathjax]\mathrm{d}t[/mathjax] vlastne nejak uplne chybi)
Offline
#8 15. 01. 2021 20:33
Re: krivkovy integral - parabola
↑ MarST:
Hezký den.
Nevidím důvod pro substituci.
Teď už jen formální úprava na základní tabulkové integrály: Odmocninu upravit na mocninu s lomeným exponentem, roznásobit závorku v integrandu a integrovat.
Pokud jsem něco nepřehlédl, tak dojdete k tady ↑ MarST: avizovanému výsledku.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » krivkovy integral - parabola (TOTO TÉMA JE VYŘEŠENÉ)

 =
=
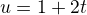
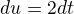
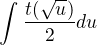 a tu som skoncil
a tu som skoncil