Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 06. 2021 17:30
Re: jednoznačné přiřazení
↑ 5dominik9:Najst explicitny predpis? Nestaci ukazat, ze take zobrazenie existuje?
Offline
#3 05. 06. 2021 17:43
Re: jednoznačné přiřazení
↑ vlado_bb: Mám napsat řešení tohoto příkladu, ale nevím, jak to sepsat.
Offline
#4 05. 06. 2021 17:44
Re: jednoznačné přiřazení
↑ 5dominik9:Je mi vcelku jasne, ze ti ide o riesenie tejto ulohy. Iba sa pytam, ci staci existencny dokaz, alebo treba explicitny predpis. Ak nevies, konzultuj zadavatela ulohy.
Offline
#5 05. 06. 2021 17:50
#6 05. 06. 2021 18:18
Re: jednoznačné přiřazení
↑ 5dominik9:Nakoniec ani to najdenie explicitneho predpisu ![kopírovat do textarea $f:[0,1] \to [0,1] \setminus Q$](/mathtex/45/455c9ec0ec076755045d651a3c26b17c.gif) nebude az take narocne. Moznosti je viac, skusim naznacit jednu z nich.
nebude az take narocne. Moznosti je viac, skusim naznacit jednu z nich.
Snazime sa  zostrojit tak, ze
zostrojit tak, ze  . To samozrejme nie je mozne pre
. To samozrejme nie je mozne pre  . Nech teda
. Nech teda  je mnozina vsetkych prvocisel. Je zrejme, ze pre kazde
je mnozina vsetkych prvocisel. Je zrejme, ze pre kazde  existuje minimalne
existuje minimalne  tak, ze
tak, ze ![kopírovat do textarea $\frac {\sqrt{p}}{n_p} \in [0,1]$](/mathtex/2d/2d49173add336582da78d2250be57fa2.gif) a tieto cisla su navzajom pre rozne
a tieto cisla su navzajom pre rozne  rozne.
rozne.
To by ti snad (ako vysokoskolakovi) malo stacit.
Offline
#7 06. 06. 2021 16:40
Re: jednoznačné přiřazení
↑ vlado_bb:
Ahoj. Nebude potom [mathjax]f(f(q))=f(q),[/mathjax] pro [mathjax]q\in Q?[/mathjax] Takze by to nebylo proste zobrazeni.
Offline
#9 20. 06. 2021 07:42
Re: jednoznačné přiřazení
↑ vlado_bb: já se moc omlouvám, ale zkouším už dva týdny nad tím uvažovat, jak jste to myslel a stále mi to není jasné. Vím, že toto přiřazení bude existovat, ale nedaří se mi ho sestrojit.
Offline
#10 20. 06. 2021 09:34 — Editoval vlado_bb (20. 06. 2021 09:36)
Re: jednoznačné přiřazení
↑ 5dominik9: Ukázal som spôsob, ako vytvoriť voľné miesta na uloženie všetkých racionálnych čísel. Treba si kresliť obrázky.
Ale to je iba jedna z možností, existuje veľa iných.
Offline
#11 20. 06. 2021 11:32
Re: jednoznačné přiřazení
↑ vlado_bb: já hlavně netuším, jak zaručit, aby se mi to zobrazovalo pouze na iracionální čísla. :-(
Offline
#12 20. 06. 2021 13:06
Re: jednoznačné přiřazení
↑ 5dominik9:Tak, ze v prvom kroku si pripravime tolko volnych miest, kolko je racionalnych cisel. Potom vsetky racionalne posleme do nich. Pripravili sme si ich tak, aby sa tieto racionalne zobrazili do iracionalnych (odmocnina z prvocisla nemoze byt racionalne cislo). Potom je to uz jednoduche.
Offline
#13 20. 06. 2021 18:25
Re: jednoznačné přiřazení
↑ 5dominik9:
1. Napřed bych si zkusil nějakým jednoduchým předpisem zobrazit všechna racionální čísla na iracionální,
např. pro [mathjax]q\in (0,1)\bigcap_{}\mathbb Q[/mathjax]
[mathjax]f(q)=q.\frac{\sqrt{2}}{2}[/mathjax]
2. Tím mi vznikne potřeba se nějak vypořádat s obrazem iracionálních čísel tvaru [mathjax]q.\frac{\sqrt{2}}{2}[/mathjax].
Tak si nadefinuju
[mathjax]f(q.\frac{\sqrt{2}}{2})=q.\frac{\sqrt{3}}{2}[/mathjax]
3. Začíná se mi rýsovat předpis pro zobrazení "ostatních" iracionálních čísel:
Pro [mathjax]x\in (0,1)\setminus \mathbb{Q}[/mathjax], [mathjax]x<>q.\frac {\sqrt{p}}{n_p} [/mathjax], [mathjax]p\in \mathbb{P}[/mathjax], [mathjax]q\in (0,1)\bigcap_{}\mathbb Q[/mathjax] bych předpokládal, že může být
[mathjax]f(x)=x[/mathjax]
(viz ↑ vlado_bb: Je zrejme, ze pre kazde  existuje minimalne
existuje minimalne  tak, ze
tak, ze ![kopírovat do textarea $\frac {\sqrt{p}}{n_p} \in [0,1]$](/mathtex/2d/2d49173add336582da78d2250be57fa2.gif) a tieto cisla su navzajom pre rozne
a tieto cisla su navzajom pre rozne  rozne.)
rozne.)
4. Bod 2 bych rozpracoval
5. Snažil bych se dokázat, že to celé bude fungovat
Hlavní je zápal, talent se dostaví!
Offline
#14 13. 08. 2021 12:45
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: jednoznačné přiřazení
Označ 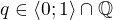 a zobraz
a zobraz
kde p je jednička nebo prvočíslo, p' je následující prvočíslo. Zbývající čísla sama na sebe.
Je tam jeden zádrhel (aspoň doufám, že jen jeden). Zkus na něj přijít a vyřešit.
Budoucnost patří aluminiu.
Offline
