Matematické Fórum

Zemish · 15. 11. 2009 14:41 — Editoval Zemish (15. 11. 2009 14:42)

Střední příčka lichoběžníku je rovoběžná s oběma základnami. Její délka je rovna aritmetickému průměru délek obou základen.

Druhou větu je třeba dokázat. Má se vycházet z podobnosti resp. shodnosti trojúhelníků.

Obr.:

Prosím, jak zapsat tento důkaz? ;-)

Doxxik · 15. 11. 2009 15:39

↑ Zemish:
postupoval bych takto:
(warning: možná moc složité)

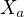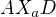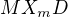1) vedl bych kolmici na základny bodem D. Tam, kde mi protne stranu a získám bod $X_a$ , tam, kde střední příčku, bod $X_{m}$ . O trojúhelnících $AX_aD$ a $MX_mD$ víme, že jsou shodné (shodují se například v pravém úhlu při bodě X (u X_m to vychází z rovnoběžnosti střední příčky a základny a) a v úhlu u bodu D (body A,M leží na jedné přímce, body X_a, X_m na jedné přímce) -> tyto trojúhelníky jsou podobné podle věty UU.
vezmeme si trojúhel. 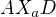$AX_aD$ . Platí v něm, že $tg(delta) = \frac{|AX_a|}{|DX_a|}$ . Obdobně to platí u trojúhelníka 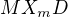$MX_mD$ : $tg(delta) = \frac{|MX_m|}{|DX_m|}$ .
Můžeme tedy využít rovnosti:
$tg(delta) = tg(delta)\nl \frac{|AX_a|}{|DX_a|} = \frac{|MX_m|}{|DX_m|}$
Dále o střední příčce víme, že leží na ose rovnoběžek, na nichž leží základny. Vzdálenost střední příčky od horní základny je tedy poloviční vůči vzdálenosti horní a dolní základny. Jelikož je přímka $DX_a$ kolmá na základny, můžeme z předcházejícího odvodit: $|DX_m| = \frac{1}{2} \cdot |Dx_a|$ . po dosazení do výše získaného vztahu získáváme:
$\frac{|AX_a|}{|DX_a|} = \frac{|MX_m|}{|DX_m|}\nl \frac{|AX_a|}{|DX_a|} = \frac{|MX_m|}{\frac{1}{2} \cdot |Dx_a|}\nl \frac{AX_a}{DX_a} = \frac{2 \cdot MX_m}{Dx_a}\nl |AX_a| = 2 \cdot |MX_m|\nl \frac{1}{2} \cdot |AX_a| = |MX_m|$ .
Totéž zopakujeme na druhé straně ( $D->C, X_m -> X_n, M ->N, A->B$ ) a získáme:
$\frac{1}{2} \cdot |BX_b| = |NX_n|$ a tedy i:
$\frac{1}{2} \cdot |AX_a| + \frac{1}{2} \cdot |BX_b| = |MX_m| + |NX_n|\nl \frac{1}{2} \cdo (|AX_a| + |BX_b|) = |MX_m| + |NX_n|$ .

Mno a protože $|BC| = |X_mX_n| = |X_aX_b|$ , jediné v čem se liší tyto 3 úsečky je vzdálenost bodu a X_{bodu}. Má tedy platit:
$|XM_m|+|XN_n| = \frac{1}{2} \cdot (|DX_d|+|CX_c| + |AX-a|+|BX_b|)\nl |XM_m|+|XN_n| = \frac{1}{2} \cdot (0 + 0 + |AX-a|+|BX_b|)\nl |XM_m|+|XN_n| = \frac{1}{2} \cdot (|AX-a|+|BX_b|)$
což jsme výše odvodili, že platí..

marnes · 15. 11. 2009 16:15 — Editoval marnes (15. 11. 2009 16:17)

↑ Zemish:
1) trojúhelníky FAM a CDM jsou shodné - věta usu
2) bod M dělí DA na stejné části
3) trojúhelníky CFB a CMN jsou podobné - věta uu
4) poměr podobnosti CFB : CMN = 2 protože M půlí CF
5) MN je tedy polovina FB a jelikož FB je součet a+c, tak je to dokázáno

Zemish · 15. 11. 2009 17:21

|DC| = |FA| (ze zadání)
|FAM| = |CDM| (střídavé úhly)
|FMA| = |CMD| (vrcholové úhly)
=> FAM = CMD (usu)

|DM| = |MA| (bod M je střed úsečky DA)
CFB - CMN (uu)
=> CFB / CMN = 2 (bod M je střed úsečky CF)
|MN| = |FB| / 2
|FB| = |FA| + |AB|
=> |MN| = (|FA| + |AB|) / 2 (=důkaz=)

OK?

marnes · 15. 11. 2009 18:18

↑ Zemish:Jo, mohlo by být

Matematické Fórum

#1 15. 11. 2009 14:41 — Editoval Zemish (15. 11. 2009 14:42)

Planimetrie (lichoběžník) - důkazová úloha

#2 15. 11. 2009 15:39

Re: Planimetrie (lichoběžník) - důkazová úloha

#3 15. 11. 2009 16:15 — Editoval marnes (15. 11. 2009 16:17)

Re: Planimetrie (lichoběžník) - důkazová úloha

#4 15. 11. 2009 17:21

Re: Planimetrie (lichoběžník) - důkazová úloha

#5 15. 11. 2009 18:18

Re: Planimetrie (lichoběžník) - důkazová úloha

Zápatí