Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivacia vyrazu s absolutnou hodnotou (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 01. 2010 20:53
Derivacia vyrazu s absolutnou hodnotou
Chcel by som Vas poziadat o pomoc s tymto prikladom:
derivacia: f(x) = e^|x(x+1)|
zrejme by som si to mal rozdelit na dve derivacie pre kladne x a pre zaporne x a vypocitat ich osobitne a nasledne spocitat derivaciu z prava, lava v nulovych bodoch absolutnej hodnoty, teda v 0 a -1. Ale vobec si neviem predstavit ako to bude cele vyzerat.
Vopred dakujem za pomoc.
Offline
- (téma jako vyřešené označil(a) halogan)
#2 06. 01. 2010 21:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivacia vyrazu s absolutnou hodnotou
↑ mato.mago:
Zdravím,
bude tak, jak navrhuješ (jen s upřesněním - ne "pro kladné x, záporné x"), ale pro nezápornou hodnotu výrazu x(x+1) - jedna derivace, pro zápornou hodnotu výrazu x(x+1) - "jiná" derivace (když to zderivuješ, tak zjistiš, že se derivace budou lišit pouze znaménkem). Jinak co do postupu výpočtu je to derivace složené funkce.
V čem konkrétně se to nezdá?
Offline
#4 06. 01. 2010 21:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivacia vyrazu s absolutnou hodnotou
↑ mato.mago:
tak zkus derivovat jen takovou funkci: 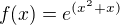
derivace složené funkce byla dnes v nočních hodinách + nová polopatická pomůcka. Standardní vzorec pro derivaci složené funkce máš?
Offline
#6 06. 01. 2010 21:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivacia vyrazu s absolutnou hodnotou
↑ mato.mago:
V pořádku, děkuji. A teď derivuj toto: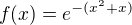
Offline
#8 06. 01. 2010 21:47 — Editoval jelena (06. 01. 2010 21:47)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivacia vyrazu s absolutnou hodnotou
↑ mato.mago:
máš jen drobný překlep v mocnine.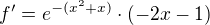
a teď jen řekni, na kterém intervalu platí derivace, co jsme počítali jako první v pořádí (kde je x*(x+1) nezáporne)
Offline
#10 06. 01. 2010 21:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivacia vyrazu s absolutnou hodnotou
↑ halogan:
tak já tady pulhodiny odblokovávám strach před absolutní hodnotou a pravě miřím k kulminaci ohledně otevřených intervalu - a co? :-)
S důvěrou přenechám kolegu do vysoce odborných rukou a myšlenek (docela se mito i hodí, děkuji) a pozdrav :-)
Ještě jsem kolegovi neřekla, že má klepat na můj zápis v TeX a pokračovat v zápisu dle pokynu.
Offline
#11 06. 01. 2010 22:00
Re: Derivacia vyrazu s absolutnou hodnotou
↑ jelena:
Tak tu je pre mna trosku problem, ale rozumiem tomu, co "halogan" napisal. Koniec koncov je to odpoved na otazku.
pre (x(x+1)) je to (-oo,1)U(0,+oo)
a pre -(x(x+1)) je to doplnok...
Derivacie v -1 a 0. Neviem ako to mam urobit.
Ale myslim, ze v tychto bodoch je derivacia rovna 0.
No neviem ako sa to pocita. Dosadenim do definicie derivacie a potom limitu alebo len dosadim body za x v derivovanej funkcii.
Offline
#12 06. 01. 2010 22:03
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivacia vyrazu s absolutnou hodnotou
Tak já to zkusím od úplného základu. Nakresli si funkci 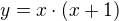 , případně
, případně 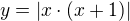 . Ona je v absolutní hodnotě a tu zkoumáš (mimo jiné).
. Ona je v absolutní hodnotě a tu zkoumáš (mimo jiné).
Měl bys dojít k následujícím poznatkům:
1) Kdy je funkce kladná? Bude na ni mít absolutní hodnota nějaký vliv?
2) Kdy bude funkce záporná? Co s ní udělá absolutní hodnota?
3) Co když bude nula? To si nech až na konec, to bude trochu složitější.
Offline
#13 06. 01. 2010 22:12
Re: Derivacia vyrazu s absolutnou hodnotou
↑ halogan:
Najprv ahoj, dakujem, ze si sa ma ujal.
Takze bude to parabola pretinajuca x-ovu os v 0 a -1.
Ked Zvazim aj absolutnu hodnotu, tak cast, ktora bola pod osou x sa preklopi nad nu.
Offline
#14 06. 01. 2010 22:16
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivacia vyrazu s absolutnou hodnotou
Dobře, je to tak.
Takže pro pro jaké x se ta funkce prakticky nemění? (otázka #1) A jaký to má vliv na derivaci?
(pokud zodpovíš správně všechny 3 otázky, tak máš hotovo)
Offline
#15 06. 01. 2010 22:20
Re: Derivacia vyrazu s absolutnou hodnotou
↑ halogan:
Nemeni sa pre x z (-oo,-1)U(0,oo)
a na derivaciu teda absolutna hodnota nema ziaden vplyv.
Offline
#16 06. 01. 2010 22:22
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivacia vyrazu s absolutnou hodnotou
Výborně!
Takže si můžeš napsat první odrážku, že pro x z té množiny je derivace (...), někde výše jsi to napsal.
Teď už jen (-1, 0) a krajní body. Co tam?
Offline
#17 06. 01. 2010 22:25
Re: Derivacia vyrazu s absolutnou hodnotou
↑ halogan:
Pre (-1,0) sa derivacia sprava ako pre by bol vyraz zaporny, teda myslim...
Teda: e^-((x^2)+1) * (-2x-1).
A v krajnych bodoch derivacia neexistuje?
Offline
#18 06. 01. 2010 22:41
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivacia vyrazu s absolutnou hodnotou
↑ mato.mago:
Jen ti tam ujelo x. Viz reakce výše - ↑ jelena:.
Derivace v nulových bodech absolutní hodnoty je trochu ošemetná. V zásadě se počítá dvěma způsoby:
1) Z definice - je to složitější a pokud funkce v daném bodě není spojitá, tak je to i nezbytné.
2) Z věty o výpočtu jednostranné derivace (strana 16, věta 45). Vypočítáš si jednostranné derivace v obou bodech a pokud se budou vždy rovnat (zprava a zleva), tak funkce má v daném bodě derivaci. Pokud budou různé, tak budou existovat jen jednostranné.
Offline
#19 06. 01. 2010 22:52 — Editoval mato.mago (06. 01. 2010 22:53)
Re: Derivacia vyrazu s absolutnou hodnotou
↑ halogan:
Takze nieco taketo: 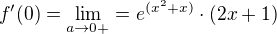
pre 0 a -1 zprava aj zlava.
Offline
#20 06. 01. 2010 23:06
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Derivacia vyrazu s absolutnou hodnotou
↑ mato.mago:
No pozor. Bude to trochu složitější.
Pro nulu zprava budeme počítat s limotou té první derivace (pro x z (-oo, -1) U (0, oo)), ale zleva budeme potřebovat už tu derivaci pro (-1, 0).
Podobně (jen obráceně) to bude pro -1. Je to jasné?
Offline
#21 06. 01. 2010 23:11
Re: Derivacia vyrazu s absolutnou hodnotou
↑ halogan:
Jasne. A v pripade, ze sa rovnaju hodnoty pre derivaciu zprava a zlava, tak je v tom bode derivacia, inak len jednostranne, ako si pisal.
Nuz, nezostava mi len sa Vam obom podakovat, velmi ste mi pomohli a Vasu pomoc si vazim.
Este raz velke VDAKA!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Derivacia vyrazu s absolutnou hodnotou (TOTO TÉMA JE VYŘEŠENÉ)