Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 11. 2009 16:52
- marnes

- Příspěvky: 11227
Dotaz na goniometrické rovnice
Dobrý den. Řešíme rovnice s polovičním argumentem, např rovnici
ja jsem zvyklej řešit pomocí substituce, tudíž není potřeba zkouška. Vyjdou tam úhly a u nich perioda 4kpí. Viděl jsem ale i řešení pomocí kde je ještě sinx v absolutní hodnotě. Když vyřeším pomocí tohoto předpisu, tak musíme umocnit - neekvivalentní úprava, tudíž zkouška.
kde je ještě sinx v absolutní hodnotě. Když vyřeším pomocí tohoto předpisu, tak musíme umocnit - neekvivalentní úprava, tudíž zkouška.
Při řešení oběma způsoby vyjdou stejné základní úhly. U 2 řešení ještě něco navíc, ale zkouška přebytečné vyloučí. V čem je problém. U druhého řešení nedělám zkoušky pro interval 2pí až 4pí, což by mě normálně nenapadlo. Takže rozdíl v řešení je ten, že se shoduju v základním úhlu, ale ne v periodě. Moje otázka tedy zní, když řeším pomocí , tak musím automaticky zdvojnásobit periodu?
, tak musím automaticky zdvojnásobit periodu?
Snad je můj dotaz k pochopení. Děkuji za čas a ochotu.
Jo. A na začátku vás zdravím.
Offline
#2 28. 11. 2009 21:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dotaz na goniometrické rovnice
↑ marnes:
jsem zastance této úpravy: 



U goniometrických funkcí se snažím substituci nepoužívat, ale rovnou řešit:

 nebo
nebo 
 nebo
nebo 



úpravy nebudu provádět, nechám to tak, aby bylo vidět, jak to vzniklo (děkuji za upozornění na chyby).
Jiný způsob bych nepoužila, jelikož bych se bala neekvivalentních úprav (u substituce bych se bala, že něco vynecham).
Je možné, že někdo z kolegů má jiný názor, přeci jen jsem utopické minulé století, navíc se vzděláním mimo EU :-)
Offline
#3 28. 11. 2009 22:04
- marnes

- Příspěvky: 11227
Re: Dotaz na goniometrické rovnice
↑ jelena:
Děkuji za reakci. Tvé řešení je pro mě srozumitelné, se stejným výsledkem, jako bych použil substituci x/2=u. I u tvého řešení vychází perioda za x1 a x2 4kpí.
V knize řešené příklady z matematiky pro střední školy ( Ján Kováčik ) je právě řešen příklad tím , kde vychází u x1 a x2 perioda 2kpí a pak provádí zkoušku. Samozřejmě mohu studentům říct, aby používali tvé metody, nebo té mé, ale připadá mi to takové surové bez vysvětlení. Nechtěl jsem je jen tak odbýt. Navíc i mě samotného to překvapilo. Třeba by stačilo říct, že když používáme daný předpis, musíme 2x zvětšit periodu. Zkusím to nějak zaonačit:-) Ještě jednou díky.
, kde vychází u x1 a x2 perioda 2kpí a pak provádí zkoušku. Samozřejmě mohu studentům říct, aby používali tvé metody, nebo té mé, ale připadá mi to takové surové bez vysvětlení. Nechtěl jsem je jen tak odbýt. Navíc i mě samotného to překvapilo. Třeba by stačilo říct, že když používáme daný předpis, musíme 2x zvětšit periodu. Zkusím to nějak zaonačit:-) Ještě jednou díky.
Jo. A na začátku vás zdravím.
Offline
#4 28. 11. 2009 22:35
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Dotaz na goniometrické rovnice
↑ jelena:
Úpravy beru, též nerad používám neekvivalentní úpravy, zvlášť u tak nevyzpytatelných (čti periodických) funkcí, jako jsou ty goniometrické.
V jednom se ale lišíme - já rád substituci. Je v ní vidět, co používám za vzorec či za úpravu. Podle mě studentům vadí (nebo se jim to zdá nepřehledné), když používají vzorec pro dvojnásobný argument, ale pracují s  , nikoliv s
, nikoliv s 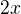 . Jistě, bystřejší to berou, ale méně chápaví mají problém i s tímto.
. Jistě, bystřejší to berou, ale méně chápaví mají problém i s tímto.
Na VŠ bych se takové úpravy nebál udělat (i když je ani tam často nestíhám :-), ale na SŠ (tím spíš na ZŠ) použil substituci.
Za závěr bych zacitoval kolegyni:
Ivana napsal(a):
Ze své zkušenosti mohu tvrdit , že 10% se opravdu něco chce naučit , 30-40% tak zvaně z musu začne na sobě pracovat a zbytek je štastný, že alespoň proleze. Je to špatné, ale je to tak.
Hezký zbytek večera přeji.
Offline
#5 28. 11. 2009 23:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dotaz na goniometrické rovnice
↑ halogan:
OT:
Řeknu jinak - mám k substituci neutrální vztah (je to operace navíc, proto z úsporných důvodu se vyhybám), ovšem když to nepůjde jinak, tak jaké já umím kreslit n-dimenzionální jablka...
Při posledním výkladu derivací složených funkcí nezabralo ani cibule z metody K-K, ani ořech, ani východní varianta, tak jsem vymyslela toto (pravda, měla jsem virozu a teplotu):
tabulková derivace: 
derivace složené funkce:  pořad byl problém, co je vnější, vnitřní atd.
pořad byl problém, co je vnější, vnitřní atd.
Vnitřní funkci jsme schovali do krabice a krabice je přelepena páskou tak, aby vzniklo x - tedy máme tabulkovou derivaci , ovšem na závěr nás zajimá, co je v krabici, tak tu pásku odstraníme a zderivujeme obsah. Krabic může být hodně.
, ovšem na závěr nás zajimá, co je v krabici, tak tu pásku odstraníme a zderivujeme obsah. Krabic může být hodně.
----------------------
Pro kolegu marnese - budu se snažit zdůvodnit svůj postup a postup pana Kováčika, co se tyče problémových míst, snad se podaří. Mějte se pěkně а спокойной ночи:-)
Offline
#6 28. 11. 2009 23:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dotaz na goniometrické rovnice
marnes napsal(a):
Třeba by stačilo říct, že když používáme daný předpis, musíme 2x zvětšit periodu.
To by nebylo moc přesné, nebyl by v tom vidět ten pravý důvod, proč se perioda může 2x zvětšit.
Je třeba si uvědomit, že když nám po důsledkové úpravě vyjde např. výsledek  , tak zkoušku neprovádíme pouze pro nějaké konkrétní
, tak zkoušku neprovádíme pouze pro nějaké konkrétní  (nabízelo by se provést zkoušku pro
(nabízelo by se provést zkoušku pro  a
a  , protože jsou z intervalu
, protože jsou z intervalu  ), ale pro všechna
), ale pro všechna  . To, že to obvykle je ekvivalentní s provedením zkoušky pro nějakých pár hodnot (např. pro ty dvě uvedené) je dáno periodicitou funkcí, které se v rovnosti vyskytují. Když budu mít rovnici (s libovolnou funkcí f)
. To, že to obvykle je ekvivalentní s provedením zkoušky pro nějakých pár hodnot (např. pro ty dvě uvedené) je dáno periodicitou funkcí, které se v rovnosti vyskytují. Když budu mít rovnici (s libovolnou funkcí f)
a dosadím do ní obecné řešení, pro které provádím zkoušku ,
,
je zřejmé, že argumenty funkce f budou pro všechna  rovna pouze sinu a kosinu v
rovna pouze sinu a kosinu v  nebo
nebo  . Pokud by tam ale byly např. siny polovičního argumentu
. Pokud by tam ale byly např. siny polovičního argumentu ,
,
tak dostaneme víc různých argumentů funkce f.
Doufám, že jsem to nepopsal moc obecně a je to ještě srozumitelné :-).
Offline
#7 29. 11. 2009 11:14
- marnes

- Příspěvky: 11227
Re: Dotaz na goniometrické rovnice
↑ BrozekP:
Děkuji za reakci a vysvětlení. Pochopil jsem to tak, že se v rovnici vyskytuje x/2, tudíž abych nezapomněl vyloučit nějaký kořen, musím provést zkoušku nebo diskuzi na intervalu 4pí ( 2x větším - protože grag funkce sin (x/2) se roztáhne právě na interval 0;4pí)
Jo. A na začátku vás zdravím.
Offline
#8 29. 11. 2009 12:50
Re: Dotaz na goniometrické rovnice
↑ marnes:
Tak nějak to bude. Ještě se vrátím k těm studentům. Kdybych toto musel vysvětlovat, vzal bych si na to grafy
Z toho je krásně vidět, že celá "struktura" řešení se opakuje s periodou "pomalejší" funkce, takže při rozboru řešení se musíme řídit touto periodou.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline