Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 02. 2010 00:03
2 slovni ulohy
asi se to nevztahuje k latce vysoke skoly, ale dostali jsme to tam
1) Petr běží kolem atletické dráhy jedním směrem a Pavel běží směrem druhým. Když víte že Petr běží 7/5 krát rychleji než Pavel, jakou poměrnou část dráhy Petr uběhne než potká Pavla poprvé?
2) Snadno se přesvědčíte, že dvě přímky v rovině vedou k nejvýše třem průsečíkům, čtyři jich maji nejvíce šest atd. Kolik je nejvyšší možný počet průsečíků pro sedm přímek v rovině?
Offline
- (téma jako vyřešené označil(a) Tychi)
#2 26. 02. 2010 09:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: 2 slovni ulohy
↑ Pjutra:
Zdravím,
1)
s_1 – draha Petra (rychlost (7/5) v)
s_2 - dráha Pavla (rychlost v),
oba běží stejnou dobu: 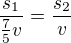 , odsud
, odsud 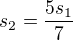
Celková dráha 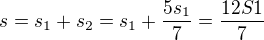 , odsud
, odsud 
Pjutra napsal(a):
Snadno se přesvědčíte, že dvě přímky v rovině vedou k nejvýše třem průsečíkům...
dopoledne jsem ochotna věřit všemu.
ale spiš jiné zadání a tak, jak navrhovalkolega Honza v tématech ZŠ.
Offline
#4 26. 02. 2010 22:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: 2 slovni ulohy
↑ Pjutra:
pokud to má být pro ZŠ nebo pro nizší ročník SŠ, tak bych použila odvozování, kolik nových průsečíku přidává další přímka:
1 přímka 0
2 přímky 1 (přidáno 1)
3 přímky 3 (přidáno 2)
4 přímky 6 (přidáno 3)....
je vidět, že tak, jak píše kolega Honza, že nová přímka protne "sadu předchozích přímek" a přidá takový počet průsečíků, kolik bylo v "sadě předchozích přímek". Tak jsem se dopracovala k číslu 21 průsečíků.
Přes kombinatoriku - průsečík vzníká ze 2 přímek, tedy kolik dvojic přímek lze vytvořit ze 7, tedy 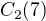 a to mi nevychází 28, jak uvádíš, ale něco jiného (ale kombinatorika není moje silná stranka).
a to mi nevychází 28, jak uvádíš, ale něco jiného (ale kombinatorika není moje silná stranka).
Offline
#6 26. 02. 2010 23:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: 2 slovni ulohy
↑ Pjutra:
není za co. Ale budoucí učitelku (je to tak?) snad by mohlo zajimat, co znamená takové zadání:
Snadno se přesvědčíte, že dvě přímky v rovině vedou k nejvýše třem průsečíkům...
Nebo bude platit argument: "Protože jsem to řekla!"? Ať se vede :-)
Offline
#8 02. 07. 2010 14:29
Re: 2 slovni ulohy
Vieme, ze 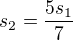 a
a  , teda
, teda 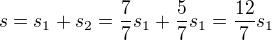 .
.
Offline