Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál fce komplexní proměnné + teorie reziduí (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 04. 2010 16:10
- dundeebrut
- Zelenáč
- Příspěvky: 3
- Reputace: 0
Integrál fce komplexní proměnné + teorie reziduí
Dobrý den,
v naprostém zoufalství se na Vás obracím s prosbou o pomoc u třech příkladů, které ať dělám co dělám, nejsem s to vypočítat.. Pokud by byl někdo z Vás ochoten obětovat kousek svého času, byl bych nesmírně vděčen.. Vzdávám tímto hold Vašim matematickým dovednostem, ty mé na to nestačí.. Zde je link:
Ještě důležita poznámka: za a v příkladu číslo 7) nutno dosadit konstantu 14, v příkladu č.8) 10, a v příkladu č.9) to bude opět 14.
Mnohokrát děkuji, třebas za vyřešení jednotlivých částí příkladů!
Dundee
Offline
- (téma jako vyřešené označil(a) Rumburak)
#2 02. 04. 2010 17:10 — Editoval Rumburak (02. 04. 2010 17:13)
Re: Integrál fce komplexní proměnné + teorie reziduí
Tak třeba k č. 7.
Je  , pokud
, pokud  .
.
Nechť M značí množinu všech komplexních kořenů rovnice
(1) 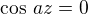 ,
,
což je zřejmě množina uzavřená v  (protože funkce cos je spojitá v
(protože funkce cos je spojitá v  ).
).
Na množině v  , která je definičním oborem fce tan = tg a množinou otevřenou v
, která je definičním oborem fce tan = tg a množinou otevřenou v  , je fce tangens holomorfní
, je fce tangens holomorfní
podle věty o derivaci podílu dvou funkcí (funkce sin, cos jsou, jak známo, holomorfní v  ).
).
Zbývá tedy vyšetřiit množinu M, tj. podat úplné řešení rovnice (1) v komplexním oboru. K tomu účelu využijeme vzorec

platný pro každé koplexní číslo  . Z rovnice
. Z rovnice  pak plyne
pak plyne
(2) 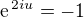 .
.
Nechť  ,
,  jsou po řadě reálná a imaginární část čísla
jsou po řadě reálná a imaginární část čísla  , tedy
, tedy  , odtud dále
, odtud dále 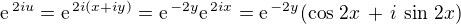 .
.
Dle (2) tedy 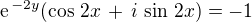 .
.
Porovnáním levé a pravé strany poslední rovnice co do reálné a imaginární části obdržíme soustavu rovnic
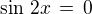 ,
,  ,
,
jejich vyřešení už patří do SŠ matematiky.
Předpokládám, že toto a formulaci závěru už zvládneš. :-)
Offline
#3 02. 04. 2010 18:43
- dundeebrut
- Zelenáč
- Příspěvky: 3
- Reputace: 0
Re: Integrál fce komplexní proměnné + teorie reziduí
↑ Rumburak:
mnohokrát děkuji, perfektní! Smekám..
Co se týče těch příkladů 8 a 9, je to složitější? Prozraď prosím alespon náznak postupu, jak na to, budu hltat každé slovo - je to pro mně existenčně důležité..
Mockrát děkuji ještě 1x za ochotu!!!
Offline
#4 05. 04. 2010 09:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál fce komplexní proměnné + teorie reziduí
↑ dundeebrut:
Zdravím,
komplexní analýzu si pamatuji opravdu velmi mlhavě - ale chtěla jsem upozornit na dosazování hodnoty a v zadání 9) - myslím, že a nemá být 14, ale a=1+4=5.
Tak, po tomto globálním sdělení můj pokus:
materiály+ další vzorové řešení od kolegy Rumburaka (kolegovi děkuji). V řešení používá jak goniometrický, tak exponenciální tvar komplexního čísla.
V zadání 8) sin(z) bych přepsala na exponenciální tvar: 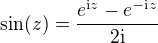
a integruje se po kružnice o poloměru t.
V zadání 9) se integruje pro kružnici o středu a (dle mého a=5), poloměru 2a=10. Může se použit Cauchy vzorce - viz odkaz v učebnici. Vychází mi, že při rozkladu (z^2-100)=(z-10)(z+10), bod z=10 leží uvnitř oblasti, ale bod z=-10 je vne oblasti - tomu se přizpůsobí i výsledek integrování.
Děkuji za spravedlivou kritiku.
Offline
#5 06. 04. 2010 08:57 — Editoval Rumburak (06. 04. 2010 13:40)
Re: Integrál fce komplexní proměnné + teorie reziduí
↑ dundeebrut:
O Velikonocích jsem nepracoval :-).
Ta úloha 8 je lehká:
Funkce sinus je holomorfní v celé komplexní rovině, k ní prímitivní funkce je (například) (- cos), proto požadovaný integrál bude roven
rozdílu (- cos B) - (- cos A), kde A je počáteční bod dané křivky, B pak její koncový bod.
EDIT.
Vyšlo mi trochu času, tak se podíváme dále.
Úloha 9 se řeší pomocí residuové věty. Integrovaná funkce má (při a = 14) singularity v bodech
(1) z = 0 ,
(2) z = 2a,
(3) z = -2a .
V případě (1) jde (s ohledem na čitatele ve zlomku) o tzv. odstranitelnou singularitu (funkci lze v tomto bodě holomorfně dodefinovat limitou),
čímž se tento případ stává pro nás dále nezajímavým.
Ve zbývajících případech jde o jednoduché póly.
Je třeba dále vyšetřit křivku 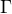 . Jde o kružnici se středem v bodě
. Jde o kružnici se středem v bodě  a poloměrem
a poloměrem 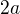 , jejíž parametrický popis je proto
, jejíž parametrický popis je proto , kde
, kde  .
.
Pól v (3) je z tohoto pohledu nezajímavý, neboť index bodu z = -2a vzhledem ke 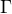 je 0 (křivka "neobíhá" zmíněný bod).
je 0 (křivka "neobíhá" zmíněný bod).
V případě (2) je index bodu z = 2a vzhledem ke 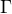 roven 1 (křivka je kladně orientovaná a "obíhá" bod z = 2a právě jednou).
roven 1 (křivka je kladně orientovaná a "obíhá" bod z = 2a právě jednou).
Je tedy třeba rozvinout integrovanou funkci v Laurentovu řadu se středem v bodě z = 2a, určit residuum, což je koeficient v této řadě
příslušný členu  , a dosadit do vzorce z residuové věty.
, a dosadit do vzorce z residuové věty.
V podstatě tedy stačí určit člen 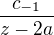 z Laurentovy řady integrované funkce, hodnota
z Laurentovy řady integrované funkce, hodnota  pak bude hledané residuum
pak bude hledané residuum
atd., jak řečeno o něco výše.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál fce komplexní proměnné + teorie reziduí (TOTO TÉMA JE VYŘEŠENÉ)