Matematické Fórum

soran · 04. 04. 2008 13:57

prosím o derivaci fce
sinx^cosx
děkuji

jelena · 04. 04. 2008 14:16 — Editoval jelena (04. 04. 2008 14:29)

↑ soran:

logaritmicke derivovani, pokud je zadani takove $(sinx)^{cosx}$ - editovano, jsou doplneny zavorky

http://matematika.havrlant.net/forum/vi … hp?id=1687 - podrobne

y = (sinx)^cosx logaritmuji levou a pravou stranu za podminky sin x vetsi 0

ln y = (cos x) * ln (sinx) derivuji levou a pravou stranu

y´/y = ((cos x) * ln (sinx))´ derivace soucinu, uvnitr slozena funkce , dal vynasobim y

y´ = ((cos x) * ln (sinx))´ * y misto y dosadim zadani funkce

y´ = ((cos x) * ln (sinx))´ * ((sinx)^cosx)

zavorka ((cos x) * ln (sinx)) se musi derivovat. OK?

Editace: neupresnila jsem, kde je mocnina - moje verze plati pro $(sinx)^{cosx}$

robert.marik · 04. 04. 2008 19:13

↑ Saturday:
Muze to byt spis jenom takova mnemotechnicka pomucka. Vsiml jsem si jak je treba Marian precizni ve vyjadrovani a jestli to cte, tak se asi pekne osypal :) Ja takovy puntickar byt nemuzu, vzhledem k tomu na jake skole pusobim, ale tohle zamavalo i se mnou ;-)

Aby to bylo v poradku, tak by bylo potreba dokazat vetu: Funkce na funkci se derivuje tak, ze "Je potřeba to derivovat jednou jako x^c (c je konstanta) a podruhe jako c^x".

A o tom, jestli to delat tak jak to delame ja a Jelena, nebo pres exponencialni funkci se tu strhla debata uz driv :)

Saturday

↑ robert.marik: No dobre, asi to radeji smazu.. Nicmene je zajimave, ze to vyslo, jak je to mozne?

Marian se z mych prispevku uz zrejme osypal tolikrat, ze to mozna uz ani radsi nepocita :-(

EDIT: zkousel jsem to i pro napr. x^x a (sin x)^x a tam to funguje taky, zkusim to jeste pro par funkci...

Lishaak · 04. 04. 2008 20:05

POZOR!!

Apeluju na vsechny, kdo toto vlakno ctou, nemazte prosim obsahy svych prispevku, jestlize na ne jiz nekdo reagoval. At uz je vas prispevek sebehorsi kvality, ostatni se mohou poucit z vasich chyb. Nehlede na to, ze odkaz toho, kdo reagoval, potom miri do prazdna. Omylem (za coz se omlouvam) jsem smazal prispevek od Saturdaye (ktery obsahoval jedine slovo: "Smazano"), a ted uz je to tady uplne rozhasene a neni jasne, na co ↑ robert.marik: reagoval.

robert.marik

Uz si nepamatuju jak to bylo, ale ono by to asi vyslo i pro obecnou funkci f(x)^(g(x)), nebo ne? Ale bez dukazu neni duvod tam strkat ty dva vzorce a jeste je navic scitat.

A ja jsem to nemyslel ve zlym. Jako mnemotechnicka pomucka to je fakt dobry (pokud to teda funguje i v tom obecnem pripade, nezkousel jsem to)

Saturday

↑ Lishaak:

Tady je muj puvodni prispevek a pripominam, ze je SPATNE, davam to sem proto, aby mel nekdo sanci napsat, kde je chyba, a s jakou vetou to koliduje
=======================================================================

Je potřeba to derivovat jednou jako x^c (c je konstanta) a podruhe jako c^x, tedy:

derivujeme jako c^x:
$(\sin x)^{\cos x} \cdot \ln(\cos x) \cdot (-\sin x)$

derivujeme jako x^c:
$\cos x \cdot (\sin x)^{\cos (x)-1} \cdot \cos x$

tedy sectenim obou vyrazu a vytknutim dostavam: $(\sin x)^{\cos x} \cdot (\cos x \cdot \cot x-\ln (\sin x) \cdot \sin x)$

=======================================================================
Kdyz se to hodi do matematickeho softu, tak ten vysledek sedi

robert.marik · 04. 04. 2008 20:30

No chyba je v uvaze:

1. vzorec $(x^c)'=c x^{c-1}$ je odvozen pro c konstantní.
2. vzorec pro derivaci c^x je $(c^x)'=c^x \ln c$ a nevidím, jak se tam ten vzorec použil. (nehledě na to, že je odvozen pro c konstantni)

Saturday · 04. 04. 2008 20:46

↑ robert.marik: Kopirovanim jsem tam udelal chybu v te derivaci.

Omlouvam se, ale toto prece neni dukaz, ze to neplati, ne? Musi se preci dokazat, ze soucet tech dvou derivaci neni roven derivaci funkce v prvnim prispevku.

robert.marik · 04. 04. 2008 21:23

Ja jsem ale nenapsal ze to nefunguje. Je to proste postup, ktery je zalozen na podivne uvaze ze jednou jednu a podruhe jinou funkci povazuju za konstatnu.

Nektere takove kvazipostupy skutecne vedou ke spravym vysldkum napriklad s derivaci $\frac{dy}{dx}$ se pri separovani diferencialnich rovnic pracuje jako s podilem i kdyz to podil neni. Je proste dokazane ze to funguje.

A ja jsem nikde nevidel dokazane ze pri derivaci vyrazu "funkce na funkci" muzu jednou derivovat tak,ze zaklad vlastne neni funkce a podruhe tak,z e exponent vlastne neni funkce. Jak jsem psal, mozna to funguje (pravdepodobne jo), ale je zalozene to na vratkych nohou (aplikuji vzorce v situaci, pro ktere nejsou odvozeny)

A podle jakeho pravidla se to secita? Proc se to treba nenasobi?

Jak se na to vlastne prislo? Ma to takto nekdo ve skriptech?

robert.marik

Takže navrhuji takové shrnutí: tři ekvivalentní metody jak derivovat výraz funkce na funkci (základ je kladný, f a g jsou funkce)

Saturdayovo derivování
$(f^g)'= g f^{g-1} f' + f^g \ln(f) g' = f^g (g'\ln f+g\frac {f'}f)$

Převod na exponenciální funkci (zastánce byl myslím Marian)
$(f^g)'= (e^{g \ln f})' = (e^{g \ln f}) (g'\ln f+g\frac {f'}f)=(f^{g}) (g'\ln f+g\frac {f'}f)$

Logaritmické derivování (zatánce byla Jelena, já to dělám taky takhle)
$y= f^g$

$\ln y= g\ln f$

$\frac{y'}y= g'\ln f +g\frac {f'}f$

${y'}= y(g'\ln f +g\frac {f'}f)=f^g(g'\ln f +g\frac {f'}f)$

Souhlas? ;)

@ Saturday: zkusil jsem to obecne a skutecne to funguje. V me hlave to ziskalo pozici mnemotechnicke pomucky jak nekomu pomoct zapamatovat si vzorec pro derivaci f^g kde f a g jsou funkce, ale neresi to problem ze nevim jak nekomu vysvetlit, jaktoze muzu pouzivat vzorec pro derivaci mocninne funkce, kdyz ten je odvozen pro mocniny kde exponentem je konstanta a ja ted mam neco jineho.

Saturday · 04. 04. 2008 21:37

↑ robert.marik: Ja jsem psal, ze to nemam odnikud prevzate, jen me zarazilo, ze to funguje.. Radsi toho uz dnes necham, bude to asi nejlepsi :))

robert.marik · 04. 04. 2008 21:47

Funguje to, taky me to prekvapilo :)

Saturday · 04. 04. 2008 21:50

Nazvěme to tedy: Saturdayeho vzorec ;-), jen skoda, ze je dnes Friday :-)

robert.marik · 04. 04. 2008 22:01

To neva VŘSR taky byla v listopadu. http://cs.wikipedia.org/wiki/%C5%98%C3% … 1_revoluce

Olin · 31. 12. 2009 14:00

Snad nevadí, že vykopávám tady to prastaré téma, narazil jsem na odkaz na něj.

Na Saturdayeho vzorec jsem před nějakou dobou přišel náhodou taky - snažil jsem se řešit jednu úlohu ohledně derivací 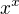$x^x$ a zajímal jsem se, jestli to nejde nějak zjednodušit. Zkusmo jsem k tomu přistoupil takto:
$f(x,y) = x^y\nl \frac{\mathrm{d}x^x}{\mathrm{d}x} = $\frac{\part f}{\part x} + \frac{\part f}{\part y}$_{y=x}$
Došel jsem k tomu nějak tak, že jsem si představil, jak v daném bodě na funkci naplácneme tu rovinu a určil jsem vztah mezi "výškou bodu" této roviny ve směru osy x, směru osy y a směru přímky y=x - je to součet (původně jsem si myslel, že by tam ještě měla nějak figurovat odmocnina ze dvou, ale praxe prokázala, že ne).

Matematické Fórum

#1 04. 04. 2008 13:57

derivace

#2 04. 04. 2008 14:16 — Editoval jelena (04. 04. 2008 14:29)

Re: derivace

#3 04. 04. 2008 19:13

Re: derivace

#4 04. 04. 2008 19:21 — Editoval Saturday (04. 04. 2008 19:43)

Re: derivace

#5 04. 04. 2008 20:05

Re: derivace

#6 04. 04. 2008 20:07 — Editoval robert.marik (04. 04. 2008 20:11)

Re: derivace

#7 04. 04. 2008 20:18 — Editoval Saturday (04. 04. 2008 20:43)

Re: derivace

#8 04. 04. 2008 20:30

Re: derivace

#9 04. 04. 2008 20:46

Re: derivace

#10 04. 04. 2008 21:23

Re: derivace

#11 04. 04. 2008 21:27 — Editoval robert.marik (04. 04. 2008 21:36)

Re: derivace

#12 04. 04. 2008 21:37

Re: derivace

#13 04. 04. 2008 21:47

Re: derivace

#14 04. 04. 2008 21:50

Re: derivace

#15 04. 04. 2008 22:01

Re: derivace

#16 31. 12. 2009 14:00

Re: derivace

Zápatí