Matematické Fórum

stativ · 31. 12. 2009 10:39

Ahojte, právě pracuji na utilitce, která bude dělat symbolickou derivaci. Derivaci dělám pomocí rekurzivní funkce nad syntaktickým stromem. Tahle funkce mi nejdřív získá operátor a pak podle daného vzorce pracuje s jeho operandy.

Ovšem narazil jsem na problém a tím je operátor ^.

Existuje nějaký vzoreček (algoritmus), co dělat když mám složenou funkci typu 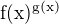$\rm{f}(x)^{\rm{g}(x)}$ ?

Díky

jelena · 31. 12. 2009 10:47

↑ stativ:

Zdravím, zřejmě potřebuješ "logaritmické derivování" - přehledné shrnutí bylo zpracováno tady. Saturdayuv vzorec vznikl přímo na tomto foru - nevím, nakolík se dostal do oficiální literatury, ale na algoritmus možna bude velmi užitečný.

Je to, co potřebuješ?

check_drummer · 31. 12. 2009 11:19

↑ stativ:

Myslím, že korektní a formální postup je použít definici obecné reálné mocniny $a^b = e^{blna}, b > 0$ , tj.
$f(x)^{g(x)} = e^{g(x)lnf(x)}, f(x) > 0$ , což lze již derivovat snadno.

stativ · 31. 12. 2009 11:50

jelena napsal(a):
↑ stativ:

Zdravím, zřejmě potřebuješ "logaritmické derivování" - přehledné shrnutí bylo zpracováno tady. Saturdayuv vzorec vznikl přímo na tomto foru - nevím, nakolík se dostal do oficiální literatury, ale na algoritmus možna bude velmi užitečný.

Je to, co potřebuješ?

Jo, přesně to. Díky moc.

stativ · 31. 12. 2009 11:52

check_drummer napsal(a):
↑ stativ:

Myslím, že korektní a formální postup je použít definici obecné reálné mocniny $a^b = e^{blna}, b > 0$ , tj.
$f(x)^{g(x)} = e^{g(x)lnf(x)}, f(x) > 0$ , což lze již derivovat snadno.

To je taky řešení, ale do programu by se mi to zabudovávalo asi hůř než ten Saturday.

check_drummer · 31. 12. 2009 12:21

↑ stativ:

...Oba postupy musí ale dát stejný výsledek (a také dají), jinak jeden z nich není správný. (Jen pozor, že f musí být kladná.)

halogan · 08. 01. 2010 12:14

↑ ploutva:

Založ si vlastní téma.

Matematické Fórum

#1 31. 12. 2009 10:39

Derivace f(x)^g(x)

#2 31. 12. 2009 10:47

Re: Derivace f(x)^g(x)

#3 31. 12. 2009 11:19

Re: Derivace f(x)^g(x)

#4 31. 12. 2009 11:50

Re: Derivace f(x)^g(x)

jelena napsal(a):

#5 31. 12. 2009 11:52

Re: Derivace f(x)^g(x)

check_drummer napsal(a):

#6 31. 12. 2009 12:21

Re: Derivace f(x)^g(x)

#7 08. 01. 2010 12:14

Re: Derivace f(x)^g(x)

Zápatí