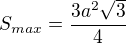Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sestrojit trojuhelník v kružnici, aby měl co největší obsah (TOTO TÉMA JE VYŘEŠENÉ)
#1 28. 02. 2011 19:53
Sestrojit trojuhelník v kružnici, aby měl co největší obsah
3)Je dána kružnice x^2+y^2=a^2 a na ní bod A=[?,a]. Sestrojíme přímku "p" rovnoběžnou s tečnou ke kružnici v bodě A. Průsečíky přímky "p" a dané kružnice označíme "B" a "C". Pro kterou přímku "p"(napište její rovnici) bude obsah trojuhelníka ABC největší? Řešte úlohu jako extrém.
Zde jsem si nakreslil kružnici, dosadil jsem bod y-ovou složku do rovnice x^2+y^2=a^2 abych získal y-lonovou. Vyšel mi bod A=[0,+-a]. A teď nevím jak přijít na to, kde má přesně přímka "p" ležet přes kružnici jako tečna, aby trojuhelník ABC měl největší obsah. Obsah trj.=z*(v/2). A taky nevím, jak to myslí, že mám úlohu řešit jako extrém. Děkuji
Offline
- (téma jako vyřešené označil(a) jelena)
#2 28. 02. 2011 20:57 — Editoval Cheop (28. 02. 2011 21:49)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:
Obrázek napoví?
Nikdo není dokonalý
Offline
#3 28. 02. 2011 21:05
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
OT: To je krásný obrázek :-) V čem je to kreslené?
Offline
#4 28. 02. 2011 21:30
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ claudia:
V programu Geogebra
Nikdo není dokonalý
Offline
#5 28. 02. 2011 21:44
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
:-( Nenapověděl :/ Ale spočítal jsem si, že ten růžový. BTW: moc pěkný obrázek !! A teďka, jak přesně zjistím, kam sečnu posunou aby obsah byl největší? Koumáme nad tím se spolubydlou ale jsme tupí :-D
Offline
#6 28. 02. 2011 21:49 — Editoval claudia (28. 02. 2011 22:03)
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:
Zkus si vyjádřit obsah toho trojúhelníku v závislosti na jeho výšce. Hledej průsečíky kružnice s přímkou y=0x+b. Ze vzdálenosti těch průsečíků od sebe spočítáš délku základny. Výšku trojúhelníku budeš znát též, v=a-b. Ze základny a výšky vyjádři obsah (v závislosti na b nebo na v, dle vkusu) a pak vztah derivuj. Kde bude mít derivace nulový bod nebo nebude existovat, budeš hledat možný trojúhelník s maximálním obsahem.
Offline
#7 28. 02. 2011 21:51 — Editoval Cheop (28. 02. 2011 21:52)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:
Ještě nápověda, který trojúhelník má při dané zakladně největší obsah?
Nikdo není dokonalý
Offline
#8 28. 02. 2011 22:05
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Cheop napsal(a):
↑ Tomaskocz:
Ještě nápověda, který trojúhelník má při dané zakladně největší obsah?
Offline
#9 28. 02. 2011 22:17 — Editoval Cheop (28. 02. 2011 22:30)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ claudia:
Tak jen taková úvaha:
Maximální délka základny - 2a = průměr kruhu
V tom případě výška = a
Obsah: 2a*a/2=a^2
Určitě existuje trojúhelník s větším obsahem.
Nebo ještě jinak:
Který rovnoramenný trojúhelník má největší obsah?
Při vědomí toho,že obsah rovnoramennéhp trojúhelníku s rameny x je: kde alfa je úhel, který svírají ramena
kde alfa je úhel, který svírají ramena
Nikdo není dokonalý
Offline
#10 28. 02. 2011 23:01
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Cheop:
Asi jsou Tvé rady nad mé chápání.
My nemáme konstatntní ani délku základny ani délku ramen, ani úhel, který svírají ramena.
Z toho vztahu by mi vyšlo, že maximální obsah je pro 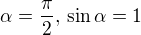 , ale to mi v této úloze též nijak nepomáhá.
, ale to mi v této úloze též nijak nepomáhá.
Offline
#11 28. 02. 2011 23:09
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Ještě hint k tomu, jak si usnadnit derivování: druhá mocnina je na nezáporných číslech rostoucí, tudíž obsah bude mít extrémy právě tam, kde bude mít extrémy druhá mocnina obsahu. Vzhledem k (očekávané) přítomnosti odmocniny je rozumnější derivovat druhou mocninu obsahu.
Offline
#12 01. 03. 2011 07:10
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ claudia:
Ještě jinak:
Který rovnoramenný trojúhelník, kterému je opsána kružnice o známém poloměru
má největší obsah?
Nikdo není dokonalý
Offline
#13 01. 03. 2011 07:42
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
No, to je předmětem oné úlohy. A dle mého výpočtu výše je to trojůhelník s výškou rovnou třem polovinám poloměru oné kružnice, s úhlem u bodu A zhruba 49°. Délka základny mi vychází 2sqrt(3) a délka odvěsen sqrt(21)a/2. Samozřejmě ten výpočet může být špatně, ale zatím nevidím důvod, proč by mělo intuitivně vycházet něco jiného.
Offline
#14 01. 03. 2011 08:37 — Editoval Cheop (14. 03. 2011 12:24)
#15 01. 03. 2011 09:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Cheop:
Zdravím a děkuji za řešení.
Trošku problém je v tom, že se jedná o samostatnou práci na VUT Brno.
Tak si, prosím, zváž, jak k tomu přistoupit, aby samostatnost byla podpořena. Zadání dostanou tak, že parametry v zadání jsou podle nějakého klíče ve skupině. Tedy tak je to univerzální návod.
Děkuji. Omlouvám se.
Offline
#16 01. 03. 2011 09:11
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ claudia:
Délka základny je: 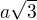
Nikdo není dokonalý
Offline
#18 01. 03. 2011 09:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Cheop:
Děkuji.
Podle dobrě miněných rad pro odpovídající máme kolegu spíše vést k řešení. Tedy v případě standardních úloh se mi zdá vhodnější rozdělit si to na kroky a projit to s kolegou krokově (pokud bude mít zájem - zdá se, že zájem má).
Tak je třeba ho v tom podpořit (celé řešení přece můžeš mít někde u sebe uložené - tak? A případně ho jednou umístit na MatWiki - s obrázkem, který každý obdivuje :-). Děkuji.
Offline
#19 01. 03. 2011 16:13
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Cheop napsal(a):
↑ claudia:
Délka základny je:
Souhlasím, počítala jsem to při snídani a zjevně ne správně :-)
Offline
#20 01. 03. 2011 17:25
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Nechci se nějak moc ztrapnit, ale stále to nechápu :-D Ale nevadí, ještě si nad to sednu a případné dotazy položím, ale za ochotu jakou projevujete Vám posílám sms za 50kč :-) Asi to nejspíš, ale nejde Vám co mi pomáháte, ale na chod webu
Offline
#21 01. 03. 2011 17:56 — Editoval claudia (01. 03. 2011 17:56)
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
Ve skutečnosti, když to pošleš na chod webu, je to dárek pro nás všechny, co jej máme rádi :-) Pomocníkům můžeš poslat nejvýše reputaci, zdarma :-)
Příklad je tady dvakrát kompletně vyřešený, takže k tomu není z mé strany mnoho, co dodat. Pokud máš pochybnosti, jestli tomu rozumíš, můžeš sem napsat, jak to tedy chápeš ty (svými slovy) a my ti můžeme napsat, zda tak je to v pořádku.
Základní myšlenka je taková, že potřebuješ vyjádřit obsah toho trojúhelníku v závislosti na jedné proměnné ( se za proměnnou pro tyto účely nepočítá, je to pouze parametr; můžeš dokonce nejprve řešit s předpokladem a=1). Vybrat si můžeš sám. Nabízí se y souřadnice přímky nebo výška trojúhelníku. Jakmile máš závislost na jedné proměnné, můžeš snadno za pomoci derivace najít, kdy je obsah maximální.
se za proměnnou pro tyto účely nepočítá, je to pouze parametr; můžeš dokonce nejprve řešit s předpokladem a=1). Vybrat si můžeš sám. Nabízí se y souřadnice přímky nebo výška trojúhelníku. Jakmile máš závislost na jedné proměnné, můžeš snadno za pomoci derivace najít, kdy je obsah maximální.
Navrhuji začít tím, že odvodíš ten vzorec pro obsah. Obsah je délka základny krát výška, z toho jedna polovina. Je tedy třeba odvodit výšku a délku základny v závislosti na tebou zvolené proměnné.
Offline
#23 01. 03. 2011 19:05 — Editoval Dana1 (01. 03. 2011 19:06)
- Dana1
- Host
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ ghostm:
a je polomer kružnice, potom Pytagorova veta pre n/2, m, polomer (a)... Trojuholník stred úsečky n = BC, bod C, bod S
#24 01. 03. 2011 19:08 — Editoval claudia (01. 03. 2011 19:09)
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
z rovnice pro přímku  a rovnice pro kružnici
a rovnice pro kružnici  zkus si vyjádřit její řešení a spočítat jejich rozdíl (tedy
zkus si vyjádřit její řešení a spočítat jejich rozdíl (tedy  ) - z obrázku je zřejmé, že rozdíl x-ových souřadnic bodů B a C je právě délka základny.
) - z obrázku je zřejmé, že rozdíl x-ových souřadnic bodů B a C je právě délka základny.
EDIT: Dana má samozřejmě snazší řešení. Ale obě varianty jsou možné.
Offline
#25 02. 03. 2011 11:10
Re: Sestrojit trojuhelník v kružnici, aby měl co největší obsah
↑ Tomaskocz:
Myslel jsem si, že už je to vyřešené, ale protože není tak tedy takto:
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Sestrojit trojuhelník v kružnici, aby měl co největší obsah (TOTO TÉMA JE VYŘEŠENÉ)

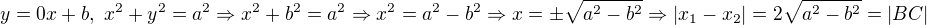


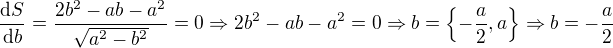

 - základna trojúhelníku
- základna trojúhelníku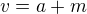 - výška trojúhelníku
- výška trojúhelníku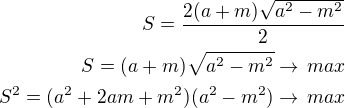
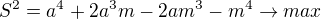 - derivujeme podle m a =0 tedy:
- derivujeme podle m a =0 tedy: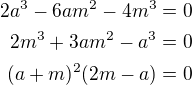
 - to bychom dostali původní přímku
- to bychom dostali původní přímku