Matematické Fórum

kiki · 05. 07. 2008 19:25

ahoj,

jsem dost v nouzi a potřebuji vypočítat tyhle příklady. Jsem zcela bezradný a potřebuju to nutně vypočítat.

1) int(1,4) dx/(1+x)* odm.x
2) int(1, nekonečno) dx/x^3+x
3) int(-nekonecno,0) x/x^3-1*dx
4)délka křivky + graf :y=1-lncosx y´= tanx x>0, x<pi/4
5) délka křivky parametricky + graf: x=t^2 y=t-t^3/3 t>0, t<odm.3

Dik t

jelena · 05. 07. 2008 20:33

↑ kiki:

Zdravim :-)

Ani jedno zadani nejde spolehlive vypocitat, jelikoz je zapsano nejednoznacne - predevsim chybi zavorky.

Pokud by toto zadani bylo v tematech zakladni skoly, tak bych byla ochotna i cist mezi radky a nabizet varianty zapisu, ale v tematech VS by mel zvladnout autor (nebo autorka?) zadani.

Dekuji.

kiki · 05. 07. 2008 21:53

↑ jelena:

pokusím se to napsat ještě jednou

1) určitý integrál od 1 do 4 dx/(1+x)*x^(1/2)
2)určitý integrál od 1 do + nekonečna dx/ x^3 + x
3) určitý integrál od mínus nekonečna do 0 x/x^4-1
4) délka křivky + graf: y=+-ln*cosx y´= tgx 0<x<pi/4
5) délka křivky parametricky + graf: x=t^2 y=t - (t^3)/3 0<t<3^(1/2)

Olin · 05. 07. 2008 22:35

Takže ty integrály jsou takto?
$\int_1^4 \frac{\mathrm{d}x}{(1+x) \sqrt x}\nl \int_1^{\infty} \frac{\mathrm{d}x}{x^3 + x}\nl \int_{-\infty}^0 \frac{x}{x^4 - 1} \mathrm{d}x$

jelena · 06. 07. 2008 00:27 — Editoval jelena (06. 07. 2008 08:56)

↑ Olin:

Doufejme :-)a dekuji za pomoc :-)

$\int_1^4 \frac{\mathrm{d}x}{(1+x) \sqrt x}$ pouzijeme substituci $\sqrt x=t$ , $\frac{\mathrm{d}x}{2\sqrt x}=dt$ ,

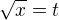po dosazeni do puvodniho zadani dostavame tabulkovy integral, nejdriv to vyresim pro neurcity, jako nalezeni primitivni funkce (a to z duvodu, ze obcas vyvstava debata - kdyz substituce, tak se musi menit i meze, tak abych tomu predesla):

$\int\frac{\mathrm{d}x}{(1+x) \sqrt x}=\int\frac{2\mathrm{d}t}{1+t^2}=2\operatorname{arctg}t + C=2\operatorname{arctg}\sqrt x +C$

$\int_1^4 \frac{\mathrm{d}x}{(1+x) \sqrt x}=2\operatorname{arctg}\sqrt x|^4_1=2(\operatorname{arctg}\sqrt 4-\operatorname{arctg}\sqrt 1)=2\left(\operatorname{arctg}2 -\frac{\pi}{4}\right)$

kalkulator to dal zvladl, zbytek necham na zitra :-)

Editace :-) ted jsem se na to podivala a nechapu, proc jsem rovnou nezmenila meze, vzdyt by to bylo daleko rychlejsi, no hrozny zvyk se vyvarovavat zmene mezi, uz to necham tak :-)

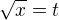Editace 2 :-) nenecham $\int_1^2\frac{2\mathrm{d}t}{1+t^2}=2\operatorname{arctg}t|^2_1$ pouzitim vyseuvedene substituce $\sqrt x=t$ doslo zmenime i meze a mame to rychlejsi (navic zmenu mezi budeme potrebovat u nevlastnich integralu), dosazovani je stejne.

jelena · 06. 07. 2008 09:52

↑ kiki:

Jelikoz v predchozim prispevku jsem resila urcity integral a nalezeni delky rovinne krivky je jeho aplikace, tak plynule navazu na zadani 4, 5.

4. y=1-ln(cosx) toto je zadani funkce,
dal je jiz vypoctena derivace zadane funkce: y´= tgx,
interval, na kterem se hleda delka, bych spise videla jako: x nalezi <0, pi/4> tedy uzavreny interval (ten otevreny se mi zda podivny, mozna nekdo z kolegu osvetli, zda to muze byt, ale nezda se to).

Pro nakresleni grafu funkce je potreba provest rychly rozbor zadane funkce:
- definicny obor je ovlivnen vyskytem logaritmu v zadani, proto (cosx) musi nabyvat pouze kladnych hodnot, coz je z vlastnosti funkce cos jasne, na kterych intervalech toto nastava.
- prirozeny logaritmus bude opakovane nabyvat na uvedenych intervalech hodnot (-oo, 0) a bude tvorit takove symetricke obloucky,
- pred ln je minus, tedy "obratime" predchozi obor hodnot zrcadlove kolem osy x,
- 1-ln(cosx) a posuneme cely graf o 1 po ose y.

Tak jsem musela postupovat hodne davno, kdyz jeste nebyla zadna moznost pouziti vykreslovacu - ted to mame snadne, nakreslila jsem to v matmat - v okrajovych bodech (kde je cosx=0) to podle meho neni dobre, ale nam to tak nevadi, jelikoz potrebujeme pouze interval <0, pi/4> a tam je to vykresleno OK, jeste pridas svisle primky pro omezeni intervalu, pro ktery se delka pocita.

$l =\int_a^b \sqrt{1 + {f^\prime(x)}^2}\mathrm{d}x=\int_0^{\frac{\pi}{4}}\sqrt{1 + {(1-lncosx)^\prime}^2}\mathrm{d}x=\int_0^{\frac{\pi}{4}}\sqrt{1 + {(tgx)}^2}\mathrm{d}x$

Vyraz pod odmocninou upravime:

$1+{(tgx)}^2=\frac{cos^2x+sin^2x}{cos^2x}=\frac{1}{cos^2x}$

$l=\int_0^{\frac{\pi}{4}}\sqrt{1 + {(tgx)}^2}\mathrm{d}x=\int_0^{\frac{\pi}{4}}\sqrt{\frac{1}{cos^2x}}\mathrm{d}x=\int_0^{\frac{\pi}{4}}{\frac{1}{cosx}}\mathrm{d}x=\frac{1}{2}ln|\frac{1+sinx}{1-sinx}|$

Jak se dosazuji meze, to jsem ukazala v predchozim vypoctu k zadani 1.

Poznamky k integrovani:
Odmocnovat jsme mohli, jelikoz cosx ma pouze kladne hodnoty.
Dalsi uprava
- donasobenim citatele a jmenovatele vyrazem cosx,
- pouziti vzorce cos^2x + sin^2 =1, substituce sinx=t
dojdeme k tomu vysledku integrovani, jak uvadim - myslim, ze se to muselo jiz pocitat - je to az moc klasicky priklad :-)

5) délka křivky parametricky + graf:

x=t^2 y=t - (t^3)/3 t nalezi <0, 3^(1/2)<

To jiz vyresil kolega thriller tady: http://forum.matweb.cz/viewtopic.php?id=3625 - je tam vytvorena funkce y, graf, zbyva pouzit vzorec na vypocet delky krivky a dovest to ke zdarnemu konci.
Pokud bude problem, tak se ozvi tady.

Poznamka k uprave: sklony nemam OK, zavorky nemam primerene velikosti, ale tato uprava je vrchol meho snazeni takto rano, tak se omlouvam :-)

jelena · 06. 07. 2008 12:10

Opet dekuji kolegovi ↑ Olin:, a pokud to neTeXoval Olin, tak si pomaham ve wikipedii, proto ten muj vysledek, nooo asi kompilat :-)
Zadani:

$\int_1^{\infty} \frac{\mathrm{d}x}{x^3 + x}$

Z wikipedie mam vzorec pro vypocet nevlastniho integralu, je potreba take k tomu precist i komentar:

$\int_a^\infty f(x)\mathrm{d}x = \lim_{b \to +\infty} \int_a^b f(x)\mathrm{d}x = A$

$\int_1^\infty \frac{\mathrm{d}x}{x^3 + x}= \lim_{b \to +\infty} \int_1^b \frac{\mathrm{d}x}{x^3 + x}\mathrm{d}x$

Integral vypocteme rozkladem na parcialni zlomky:

$\int\frac{\mathrm{d}x}{x^3 + x}\mathrm{d}x=\int\frac{\mathrm{d}x}{x(x^2 + 1)}\mathrm{d}x$

mame jak realny koren x=0, tak i imaginarni koreny, proto se integrovana funkce se rozlozi do tvaru:

$\frac{1}{x(x^2 + 1)}=\frac{A}{x} + \frac{Bx+C}{x^2 + 1}$

Dal uz zadnou prekazku nebo zadrhel nevidim, pokud prece jen nastane, tak se ozvi tady.

Stejny zpusob bych pouzila i u zadani 3 a take tam ocekavam rozklad na parcialni zlomky.

Hodne zdaru :-)

kiki · 06. 07. 2008 12:35

↑ jelena:

chápu správně, když x dosadím rovnice y a potom to zderivuju a pak dosadím do vzorce délky křivky????????????
Můžu alespoň z tebe vymámit správný výsledek pro kontrolu??????????????
dík

jelena · 06. 07. 2008 12:59

↑ kiki:

Pokud to je otazka k zadani 5, tak je to tak, ze z parametrickeho zadani funkce jiz je udelan prevod na zadani bez parametru. To znamena, ze je to uplne stejny postup pro vypocet, jako zadani 4 - tedy derivace, dosazeni do vzorce pro delku krivky, integrovani atd.

kiki napsal(a):
↑ jelena:
Můžu alespoň z tebe vymámit správný výsledek pro kontrolu??????????????

Pro kontrolu se daji pouzit online zdroje - ja treba hodne pouzivam wims

nebo nase oblibena stranka pana Roberta Maříka

kiki · 06. 07. 2008 13:55

↑ jelena:
Ahoj Jeleno,

mám skromný dotaz jak u pana maříka nebo ve wimsu napsat odmocninu. Zkouším to jak nejlíp umím a nemůžu na to příjít.
Dík

jelena · 06. 07. 2008 14:16

↑ kiki:

Urcite tam funguje tato moznost x^(1/2)

Skutecne se musi davat pozor na spravny pocet zavorek. Jak ve wims, tak u pana Marika je navadeno, v pripade chybneho zadani - bud vypisem nebo se da zmacknou tlacitko "Preview" - napravo od okna zadani a vse se ukaze, zda je to OK.

kiki · 06. 07. 2008 19:49

↑ jelena:
Ahoj Jeleno,

s parciálními zlomky se trápím celé odpoledne a nic. Mohla by si mi s tím pomoci???????????????

jelena · 06. 07. 2008 20:29 — Editoval jelena (07. 07. 2008 08:00)

↑ kiki:

Neuvadis sice, co je konkretni problem, tak to vezmu cele, ale trochu hopem, nemam moc casu:

Ted jsem to zkusila projet krokove s napovedou od pana Maříka a funguje to pekne, pochvalim :-)

Tady je moje rucni prace:

$A(x^2 + 1) + (Bx+C)x=Ax^2+A+Bx^2+Cx=x^2(A+B)+Cx+A$

ted to porovnam s puvodnimi koeficienty v zadani a resim jako takovou malou soustavu rovnic:

x^2(A+B) = 0*x^2 odsud (A+B) = 0

Cx = 0*x odsud C=0

A = 1, dosadim do (A+B) = 0, odsud B = -1

$\frac{1}{x} + \frac{-x}{x^2 + 1}$ - toto mam integrovat - prvni je hned tabulkovy na ln |x|, druhy po substituci

x^2 = t take na ln .... + uprava ln

$\int f(x)dx= \ln \left|x\right| - { 1 \over 2} \ln \left(x^2 +1 \right)=\ln \left(\frac{x}{\sqrt{x^2 +1}} \right)$

Ted je potreba dle navodu ve wikipedii zjistit limitu, nejdriv dosadit meze (b, 1), pak vidime:

b se blizi nekonecnu - limita je 0, po dosazeni 1 to je ln(1/sqrt(2)). Dostavame vysledek lim 0-ln(1/sqrt(2))=-ln(1/sqrt(2)), limita existuje a je to konkretni cislo cca 0,35 (limita vlastni).

Zadani 3 je uplne stejne. Bohuzel, ted nemam cas - tak bud nekdo z kolegu, nebo az pozdej (asi dost pozdej :-) Doufam, ze na to nekdo koukne pro pripadnou opravu, predem dekuji :-)

editace - opravila jsem vysledek limity, velka chyba tam byla :-(

jelena · 07. 07. 2008 16:54

Opravila jsem v predchozim prispevku svuj vypocet limity, pekna chyba to byla, omlouvam se - spech je, bohuzel, spatny pritel :-(

jelena · 07. 07. 2008 23:20

K tomuto zadani jeste pridam graf, ze ktereho je videt co se pocitalo pomoci nevlastniho integralu:

$\int_1^{\infty} \frac{\mathrm{d}x}{x^3 + x}$

http://forum.matweb.cz/upload/718-nevl.JPG - je to pochopitelne takovy naznak :-)

K zadani 3:

$\nl\int_{-\infty}^0 \frac{x}{x^4 - 1} \mathrm{d}x$

rozklad jmenovatele pro vypocet pomoci parcialnich zlomku vypada takto (x-1)(x+1)(x^2+1) a je videt, ze na intervalu, kde se ma integrovat je jeden z bodu nespojitosti (-1).

Obrazek : http://forum.matweb.cz/upload/212-nevl2.JPG

Matematické Fórum

#1 05. 07. 2008 19:25

pár příkladů na vypočítání

#2 05. 07. 2008 20:33

Re: pár příkladů na vypočítání

#3 05. 07. 2008 21:53

Re: pár příkladů na vypočítání

#4 05. 07. 2008 22:35

Re: pár příkladů na vypočítání

#5 06. 07. 2008 00:27 — Editoval jelena (06. 07. 2008 08:56)

Re: pár příkladů na vypočítání

#6 06. 07. 2008 09:52

Re: pár příkladů na vypočítání

#7 06. 07. 2008 12:10

Re: pár příkladů na vypočítání

#8 06. 07. 2008 12:35

Re: pár příkladů na vypočítání

#9 06. 07. 2008 12:59

Re: pár příkladů na vypočítání

kiki napsal(a):

#10 06. 07. 2008 13:55

Re: pár příkladů na vypočítání

#11 06. 07. 2008 14:16

Re: pár příkladů na vypočítání

#12 06. 07. 2008 19:49

Re: pár příkladů na vypočítání

#13 06. 07. 2008 20:29 — Editoval jelena (07. 07. 2008 08:00)

Re: pár příkladů na vypočítání

#14 07. 07. 2008 16:54

Re: pár příkladů na vypočítání

#15 07. 07. 2008 23:20

Re: pár příkladů na vypočítání

Zápatí