Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 03. 08. 2008 19:33 — Editoval ttopi (03. 08. 2008 19:39)
Re: Nerovnice, nulové body
Já to řešil normálními úpravami a vyšlo mi 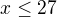 .
.
Metoda nulových bodů by mohla být metoda, při které se neorvnice upraví na takový tvar, aby byla součinem závorek a na druhé straně 0. Pak se nulové body rovnají těm číslům, která po dosazení do závorek dávají 0.
Dám vymyšlený příklad. 
Tady jsou nulové body -3 a 2. Pak se řeší intervali mezi - nekonečnem;-3;2 a +nekonečnem.
EDIT: Tak ten výsledek je špatně, ještě se na to podívám.
oo^0 = 1
Offline
#5 03. 08. 2008 19:48
Re: Nerovnice, nulové body
Nejdříve upravme nerovnici tak, aby na jedné straně byl podíl a na druhé 0. Takže
Nulovými body nazvěme reálná čísla, po jejichž dosazení se čitatel nebo jmenovatel rovná 0. Množinu všech reálných čísel zapsanou pomocí intervalu  rozdělíme pomocí nulových bodů (v našem případě 3, -3 a 27) na několik podintervalů a to tímto způsobem:
rozdělíme pomocí nulových bodů (v našem případě 3, -3 a 27) na několik podintervalů a to tímto způsobem:
- nulové body, pro které je jmenovatel roven 0 z podintevalů vyloučíme
- nulové body, pro které je čitatel roven 0 z podintervalů vyloučíme tehdy, pokud řešíme "ostrou" nerovnost, tj. se znaménkem  , nebo
, nebo  . V případě "neostré" nerovnosti (
. V případě "neostré" nerovnosti (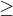 resp.
resp. 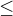 ) budeme s těmito body v podintervalech počítat.
) budeme s těmito body v podintervalech počítat.
V našem případě rozdělíme množinu reálných čísel na tyto intervaly: 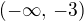 ,
,  ,
, 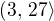 ,
, 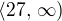 . Určeme dále znaménko čitatele a jmenovatele na jednotlivých intervalech tím, že dosadíme libovolný vnitřní bod z příslušného intervalu do výrazu na levé straně nerovnosti.
. Určeme dále znaménko čitatele a jmenovatele na jednotlivých intervalech tím, že dosadíme libovolný vnitřní bod z příslušného intervalu do výrazu na levé straně nerovnosti.
1. V intervalu 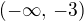 zvolme např. -4 a dosaďme do levé strany. Dostáváme
zvolme např. -4 a dosaďme do levé strany. Dostáváme 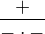 , čitatel je kladný a jmenovatel kladný (
, čitatel je kladný a jmenovatel kladný (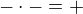 ), a tedy celý zlomek je kladný.
), a tedy celý zlomek je kladný.
2. V intervalu  zvolme např. 0 a dosaďme do levé strany. Dostáváme
zvolme např. 0 a dosaďme do levé strany. Dostáváme  , čitatel je kladný a jmenovatel záporný (
, čitatel je kladný a jmenovatel záporný (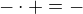 ), a tedy celý zlomek je záporný.
), a tedy celý zlomek je záporný.
3. V intervalu 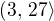 zvolme např. 10 a dosaďme do levé strany. Dostáváme
zvolme např. 10 a dosaďme do levé strany. Dostáváme  , čitatel je kladný a jmenovatel kladný (
, čitatel je kladný a jmenovatel kladný ( ), a tedy celý zlomek je kladný.
), a tedy celý zlomek je kladný.
4. V intervalu 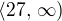 zvolme např. 30 a dosaďme do levé strany. Dostáváme
zvolme např. 30 a dosaďme do levé strany. Dostáváme  , čitatel je záporný a jmenovatel kladný (
, čitatel je záporný a jmenovatel kladný ( ), a tedy celý zlomek je záporný.
), a tedy celý zlomek je záporný.
Nerovnici 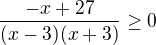 jsme tedy řešili tak, že jsme hledali reálná čísla, pro něž je výraz
jsme tedy řešili tak, že jsme hledali reálná čísla, pro něž je výraz  kladný nebo nulový. Ze "znaménkové diskuze" vyplývá, že tomuto vyhovují reálná čísla náležící intervalům
kladný nebo nulový. Ze "znaménkové diskuze" vyplývá, že tomuto vyhovují reálná čísla náležící intervalům 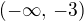 a
a 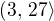 , tedy
, tedy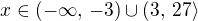 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 03. 08. 2008 23:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nerovnice, nulové body
↑ Ivana:, ↑ ttopi:
Zdravím vás :-)
Možné důvody, že vaše řešení nebylo uplně kompletní jsou asi:
- podstatný důvod - v letě máte nárok na odpočinek :-)
- méně podstatný důvod - ze základní školy se přenáší "takový skoro bych řekl(a) ...nepěkná věc" - násobení jmenovatelem při řešení rovnic s neznamou v jmenovateli.
Potom na střední se to musí napravovat u nerovnic. Já to řeším u mnou doučovaných takto - hned u rovnic s neznamou v jmenovateli zakazuji nasobit jmenovatelem a trvám na tom, aby rovnice převáděli do anulovaného tvaru, pak aby napsali podmínku, kdy zlomek bude 0 (čitatel 0, jmenovatel nesmí být 0). Brblají, že to ve škole není potřeba, ale na tom trvám.
Potom u nerovnic už takový problém nemusím řešit, už nenásobí, ale rovnou převádějí do anulovaných tvarů. A jen doladím tabulku (znamenka).
Dokonce jsem byla dřív tak tvrdá, že meli zapisovat cely výrok, kdy zlomek nabývá třeba kladných hodnot, ve smyslu " kdyz... vetší a zároveň ..... větší nebo ...menší a zároveň ... menší", ale od toho už jsem opustila :-( Ale to je z jiného tématu :-)
Jinak tady na foru je hodně vyřešených nerovnic jak součinových, tak i podilových (a určitě i od vás, pěkně vyřešených :-).
Tak si užívejte odpočinku a mějte se pekně :-)
Offline
#10 06. 08. 2008 14:10 — Editoval lukaszh (06. 08. 2008 14:16)
Re: Nerovnice, nulové body
↑ Zbyšek:
Keďže 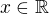 , potom sa nerovnica nesmie rieši? prenásobením ako rovnica. Úpravami dostaneš:
, potom sa nerovnica nesmie rieši? prenásobením ako rovnica. Úpravami dostaneš:
Treba si stanovi? nulové body: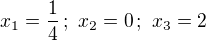
Nerovnicu si zapíšem v tvare 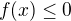 , iba pre uľahčenie zápisov :-) Teraz si rozpíšeš jednotlivé intervaly podľa nulových bodov a zistím, kde f(x) nadobúda kladné, resp. záporné hodnoty. My však podľa zadania potrebujeme hodnoty záporné nanajvýš rovné nule:
, iba pre uľahčenie zápisov :-) Teraz si rozpíšeš jednotlivé intervaly podľa nulových bodov a zistím, kde f(x) nadobúda kladné, resp. záporné hodnoty. My však podľa zadania potrebujeme hodnoty záporné nanajvýš rovné nule:
Odtiaľ vyplýva, že 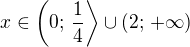 aby bola splnená podmienka zo zadania.
aby bola splnená podmienka zo zadania.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#12 06. 08. 2008 16:37
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Nerovnice, nulové body
↑ Zbyšek:Dokud je v čitateli co roznásobovat, roznásobuj. Až tam nejsou žádné závorky, zbude tam většinou lineární dvojčlen:
ax+b
nebo kvadratický trojčlen:
ax^2+bx+c,
případně polynom většího stupně.
Nulové body jsou pak kořeny tohoto polynomu, v prvním případě tedy -b/a, ve druhém 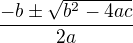 .
.
V případě polynomů vyššího stupně se na to musí nějak fikaně, ale to tě na běžné střední škole nepotká (a pokud jo, tak si možná vzpomeneš na postup hledání racionálních kořenů polynomu).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#15 13. 08. 2008 16:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nerovnice, nulové body
↑ zidulin:
Zdravím :-)
Prosím:
1) pro novou otázku nové samostatné téma, jinak je to nepřehledné.
2) není nutné nařízovat způsobem "Určete množinu ..." - lepší je sdělit pro ostatní, co potřebuješ vysvětlit a v čem je problém při řešení
Děkuji :-)
Máš nerovnici s absolutní hodnotou - nejdřív je potřeba trochu upravit:
|x-2|-2|x-2|>2-3
-|x-2|>-1 (násobím (-1) - změním "vetší" na "menší")
|x-2|<1 ted je potřeba řešit buď graficky nebo odstaraněním absolutní hodnoty pomocí nulového bodu x= 2
Nerovnic s absolutní hodnotou je tada na foru hodně - zkus projit odkazy :
http://forum.matweb.cz/viewtopic.php?id=1621
http://forum.matweb.cz/viewtopic.php?id=2110
Hodně zdaru :-)
Offline