Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Integrály - odvození vzorce pro obsah koule (TOTO TÉMA JE VYŘEŠENÉ)
#2 11. 05. 2009 17:32 — Editoval ttopi (11. 05. 2009 17:33)
Re: Integrály - odvození vzorce pro obsah koule
Já to teď na praxi odvodil podle Archimeda a moc se to líbilo :-)
Protože archimedes přišel na to, že když do plného válce vody o výšce 2r a poloměru podstavy r vložíme kouli o poloměru r, vyteče nám 2/3 obsahu vody a tedy, že poměr objemu koule ku objemu válci se rovná 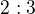 . Pak tedy vemu vzorec pro objem tohoto válce, který je
. Pak tedy vemu vzorec pro objem tohoto válce, který je 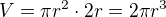 a vynásobím ho
a vynásobím ho  a dostávám objem koule
a dostávám objem koule 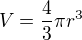 :-))
:-))
oo^0 = 1
Offline
#3 11. 05. 2009 18:06
- svatý halogan
- Příspěvky: 243
- Reputace: 0
Re: Integrály - odvození vzorce pro obsah koule
Mějme rovnici kružnice: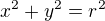
Vyjádříme si y^2 jako 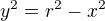
A použijeme vzorec pro výpočet objemu obrazce, který rotujeme kolem osy x. Budeme integroval od nuly do r - tí získáme polokouli. Poté vynásobíme dvěma a máme hotovo.
Vyjde to pěkně (a správně :)
Offline
#4 11. 05. 2009 22:35
Re: Integrály - odvození vzorce pro obsah koule
↑ ttopi:
Tak toto som ešte nepočul, ale veľmi sa mi to páči :-D Ten Archimedes bol fakt hlavička, a my sa tu oháňame nejakým zložitým kalkulom ;-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 12. 05. 2009 06:58
Re: Integrály - odvození vzorce pro obsah koule
↑ lukaszh:
Mě se to také líbí. Obecně platí, že poměr válce:koule:kuželi je 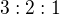 za předpokladu, že kužel i válec mají stejnou výšku a poloměr podstavy a koule má stejný poloměr jako podstava válce a výška všech 3 těles je 2r. Takže i pro kužel z toho odvodíš krásně vzorce :-)
za předpokladu, že kužel i válec mají stejnou výšku a poloměr podstavy a koule má stejný poloměr jako podstava válce a výška všech 3 těles je 2r. Takže i pro kužel z toho odvodíš krásně vzorce :-)
To samé platí pro povrch, ale tam se to nedá ukázat s vodou, tam je to horší :-)
Vypadá to nějak takto 
oo^0 = 1
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Integrály - odvození vzorce pro obsah koule (TOTO TÉMA JE VYŘEŠENÉ)
