Matematické Fórum

Nathaniel · 04. 03. 2010 11:44

Dobrý den pomůže mi někdo, jak mám postupovat? Díky

Olin · 04. 03. 2010 15:32

Už jsme tady jedou řešili jedno velmi podobné zadání. I toto je neúplné - co značí $a_{n+m} = e$ ? To má platit pro všechna n, m nebo pro něco konrétního nebo jak?

Nathaniel · 04. 03. 2010 18:50

↑ Olin:

Aha musel nám to zadávat stejný přednášející, zadal jen tyto příklady na tabuli a nic k tomu neřekl...

jelena · 07. 03. 2010 12:51

↑ Nathaniel:

jelikož i v odkazovaném tématu je záhadou "e", tak se ptám, skutečně "nic neřekl"? nebo to "e" opravdu vyslovil? Neb něco mi říká, že to není e, ale $l$ . Děkuji.

Nathaniel · 07. 03. 2010 16:02

↑ jelena:

to "e" neřekl napsal obadva příklady na tabuli, tudíž je možné, že jsme to obadva špatně opsali a mělo to bejt l .. jak by se to vtom případě řešilo ? díky za odpověď

jelena · 08. 03. 2010 21:33

↑ Nathaniel: nechat se inspirovat v odkazovaném tématu - z tohoto záhadného zadání ovšem plyne jen ponaučení - máte se pořádně zeptat, co se od vás očekává.

Nějak pochybuji, že vzejde i něco jiného, než toto doporučení.

Nathaniel · 12. 03. 2010 14:13

tak jsem za nim zasel, aby me to vysvetlil a rekl ze zadani je spravne :( a vic mi ktomu nerekne protoze to je muj projekt ale pak mi ktomu napsal toto:

an=a1 +(n-1) *d

an+m= a1+ (n+m -1)*d

e=k + (n+m -1)*d

jeste nez me tohle napsal tak jsem ja u tabule udelal to co v tom podobnem prispevku :

a(n+m)=e

a(n+m+1)=a(n+m)+d

a(n+m+1)=e+d

a jen sem mu rekl ze proto se e=k ale rekl me ze to ne ale ze do toho e+d jsem to mel spravne..

nevi nekdo jak to dokoncit ? diky

pietro · 12. 03. 2010 14:48

↑ Nathaniel:
ked teda a(n+m)= a1+(n+m-1)*d=k+(n+m-1)*d ==> d= (e-k)/ (n+m-1) a aritm.postupnost je urcena, vieme dva body, jednaj a1 a tiez d=difer. Zelany predpis by mohol byt a(n+1)= an +(e-k)/(n+m-1) , je to divne ale asi tak?

Pavel · 12. 03. 2010 15:03 — Editoval Pavel (12. 03. 2010 16:19)

↑ Nathaniel:

Celý příklad je nekorektně zadán. Není vůbec jasné, co jsou ty indexy 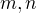$m,n$ zač. Vysvětlil bych mu to polopaticky. Pokud o $m$ nic nevím, tak předpokládám, že to $m$ může být libovolné. Pak $a_{n+m}=e$ platí pro libovolné 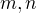$m,n$ .

$a_{n+1}=e,\qquad a_{n+2}=e\qquad\Rightarrow\qquad a_{n+2}=a_{n+1}+d\qquad\Rightarrow\qquad e=e+d\qquad\Rightarrow\qquad d=0.$

Pak

$a_n=a_1+(n-1)d=k+(n-1)\cdot 0=k\ \forall n\in\mathbb{N}\qquad\Rightarrow\qquad a_{n+m}=k\qquad\Rightarrow\qquad k=e.$

Pokud takové $m$ existuje jedno jediné, pak $a_{n+m}=e$ platí pro libovolné $n$

$a_{1+m}=e,\qquad a_{2+m}=e\qquad\Rightarrow\qquad a_{2+m}=a_{1+m}+d\qquad\Rightarrow\qquad e=e+d\qquad\Rightarrow\qquad d=0.$

Pak

$a_n=a_1+(n-1)d=k+(n-1)\cdot 0=k\ \forall n\in\mathbb{N}\qquad\Rightarrow\qquad a_{n+m}=k\qquad\Rightarrow\qquad k=e.$

jelena · 12. 03. 2010 16:12

↑ Pavel:

Zdravím, proč je $a_{n+m}=0$ ? Děkuji.

Pavel · 12. 03. 2010 16:19

↑ jelena:

Děkuji za upozornění, je to překlep. Už jsem to spravil.

jelena · 12. 03. 2010 20:47

↑ Pavel: děkuji, nebyla jsem si jistá, kde se to mohlo najit v zadání.

A když už se tomu tak vznešeně říká "projekt", tak snad i zadání "projektu" mohlo mít odpovídající formu, ale nemám nárok to posuzovat.

petrkovar · 12. 03. 2010 21:27

↑ pietro:Já myslím, že vzhledem k zadání a konzultaci s vyučujícím je pietrův výpočet správně. Pokud není nic víc řečeno, tak beru písmenka jako parametry a jediné, co potřebuji vyjádřit (ne vyčíslit!) je d. To pietro udělal a do rekurentního vztahu dosadil.
Zadání chápu tak, že máme aritmetickou psloupnost s prvním členem $k$ a (n+m)-tým členem $e$ . Zbývá určit diferenci $d$ , která samozřejmě na $k$ , $e$ i $n+m$ závisí.
Podobně se bude řešit i druhý zmíněný příklad.
Kdo je vyučující?

Nathaniel · 13. 03. 2010 14:38

díky všem za pomoc

Matematické Fórum

#1 04. 03. 2010 11:44

Aritmetická posloupnost

#2 04. 03. 2010 15:32

Re: Aritmetická posloupnost

#3 04. 03. 2010 18:50

Re: Aritmetická posloupnost

#4 07. 03. 2010 12:51

Re: Aritmetická posloupnost

#5 07. 03. 2010 16:02

Re: Aritmetická posloupnost

#6 08. 03. 2010 21:33

Re: Aritmetická posloupnost

#7 12. 03. 2010 14:13

Re: Aritmetická posloupnost

#8 12. 03. 2010 14:48

Re: Aritmetická posloupnost

#9 12. 03. 2010 15:03 — Editoval Pavel (12. 03. 2010 16:19)

Re: Aritmetická posloupnost

#10 12. 03. 2010 16:12

Re: Aritmetická posloupnost

#11 12. 03. 2010 16:19

Re: Aritmetická posloupnost

#12 12. 03. 2010 20:47

Re: Aritmetická posloupnost

#13 12. 03. 2010 21:27

Re: Aritmetická posloupnost

#14 13. 03. 2010 14:38

Re: Aritmetická posloupnost

Zápatí