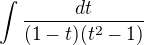Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 03. 2010 13:07
integrál
Ahoj nemůžu přijít na jeden příklad, včera mi tady někteří radili a myslím že dobře ale prof. se můj zápis moc nelíbil a já nevím proč. Tak jesttli víte kde je chybka byl bych rád kdyby jste mi poradili. díky
Takhle jsem to napsal ( tužka je od prof. )
http://forum.matweb.cz/upload/1269947201-DSCI3199.JPG
Offline
- (téma jako vyřešené označil(a) berka33)
#2 30. 03. 2010 15:02
#4 30. 03. 2010 15:14
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: integrál
to co je v krouzku je vlastne nesmysl, protoze tam je integral z funkce dvou promennych. Melo by se dodrzovat to, ze v integralu je promenna bud jenom x nebo jenom t a nemichat to. V jednom integralu se x a t nema jak sejit.
Offline
#6 30. 03. 2010 15:35
Re: integrál
↑ kaja(z_hajovny):
To já chápu že se to nemá takhle dělat, ale nevím jak to taam dosadit tu substituci aby to vycházelo tak jak má. Mám v tom nějaký zmatek
Offline
#7 30. 03. 2010 15:41
Re: integrál
tady mám ten začátek toho příkladu který jsem dělal ted je tam nějaká chybka? já nemůžu přijít na to jak s tím jmenovatelem proč tam máš ten sin na 4
http://forum.matweb.cz/upload/1269956494-DSCI3200.JPG
Offline
#9 30. 03. 2010 20:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrál
↑ berka33:
Zdravím,
toto od ↑ kaja(z_hajovny): je jasné?
pokračuji úpravy:
v jmenovateli je vzorec 

je to ten výsledek, co má být?
nebo má být tento?
berka33 napsal(a):
1/(t+1)(t^ 2-1)dt
Offline
#12 30. 03. 2010 22:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrál
↑ berka33:
úplně na začátek, když provádíme substituci, máme t=cos(x), dt=-sin(x)dx. Tedy my potřebujeme mít sin(x) v čitateli. Pak můžeme nahradit -sin(x)dx za dt. Proto čitatel a jmenovatel násobíme sin(x).
A proto v čitateli už můžeme nahrazovat za dt a nevzniká 2 různé promenné a v jmenovateli je 
V pořádku?
Offline
#14 30. 03. 2010 22:38 — Editoval jelena (30. 03. 2010 22:38)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrál
↑ berka33:
"Normálně" donásobím čiatele a jmenovatele sin(x) a normálně donásobím čitatele a jmenovatele (-1). Teď si vezmu barevnou propísku a v čitateli zakroužkuji -sin(x)dx. Tento výraz nahradím dt. Zbytek (nový sin(x) v jmenovateli a (-1)) mi zůstane do integrovaného výrazu.
Není možné čitatel násobit (+sin(x)) a jmenovatel (-sin(x)) nebo naopak. Můžeme násobit (rozšířovat) pouze úplně stejným výrazem (i včetně znamének).
A zároveň provádím nahrazení dt a t, aby nebylo různých promenných v jednom zápisu.
V pořádku?
Offline
#16 30. 03. 2010 22:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrál
Také děkuji za celý kolektiv trpelivých :-)
Když se podívaš na ten svůj první papír ↑ berka33:, tak kdybys nešokoval učitelku sin^2(x) v jmenovateli a rovnou ho nahradil (1-t^2), tak není co řešit.
Ať se vede.
Offline
#18 30. 03. 2010 23:31 — Editoval jelena (01. 04. 2010 00:05)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrál
↑ Tychi:
Zdravím,
za to nemůžeš, kolega to asi nedočetl a navíc nás mohl odkázat, že včera se to řešilo, a ne celé od začátku. A že nedočetl - máš v poznámce užito slovesa v času minulém a podle toho by mělo být i znění v reputaci. Důkaz.
Umí vážené Moderátorstvo opravit sloveso u Tychi v reputaci? Děkuji.
EDIT: o schopnostech moderátorů jsem ani okamžík nepochybovala, děkuji :-)
Offline
#19 31. 03. 2010 23:51
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: integrál
↑ jelena:
Slovesa opravena.
Offline
 tak mi vyjde po úpravách:
tak mi vyjde po úpravách: