Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 12. 06. 2010 08:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kružnice
Zdravím vás,
kolega ↑ pietro: má postupovo stejně, ale byl trochu nepozorný při čtení zadání (přehodil, která vzdálenost j větší). Ale zas byl dost odvažny, co se týče zápisu řešení v sekci SŠ.
------
не пробуждай, не пробуждай....
Offline
#6 12. 06. 2010 09:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kružnice
↑ zdenek1:
Já vím, že víš :-) ale kde je alespoň řádka komentáře ke kolegovi? A nedramatizuj postoje zoufalých "tazatelů".
Je velmi horko, však proto posílám alespoň imaginární sníh (a udatného Denisa Davydova). Potěšující i v tom horku je, že jako zcela osvobozená Věra Pavlovná mohu se zcela svobodně rozhodnout, v jakém pořadí seřadím své dnešní úkoly - zda se mi chce nejdřív dopsat rozbor, nebo zda nejdřív žehlit a proložit to umýváním podlah.
Pro začátek zcela svobodně vyhlásím konec OT a zdravím srdečně :-)
Offline
#8 12. 06. 2010 10:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kružnice
↑ pietro: mazaním příspěvku narušuješ myšlenkovou souvislost (která i tak silně narušena horkem).
Můj příspěvek pro kolegu Zdeňka má takový původ.
Zdeňkovi jsem poslala trochu sněhu, Tobě pošlu trochu vody od Айвазовского a Лермонтова. Na plávání by to mělo stačit a davej na sebe pozor, až vypluješ na šíre moře (chemiku je tady velký nedostatek :-)
Offline
#12 12. 06. 2010 22:49 — Editoval jelena (12. 06. 2010 22:54)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kružnice
↑ amater:
Množina bodů vzdalených od počátku leži na kružnici  , množina bodů vzdálených od bodu A=(-3,6) leží na kružnici
, množina bodů vzdálených od bodu A=(-3,6) leží na kružnici  a plati, že
a plati, že 
Ovšem ve výsledku má být elipsa (což kolega Zdeněk také má, ale pojmenoval to "kružnice") a já jsem to zkontrolovala. No jo.
EDIT: já už překontrolovana, omluva, nevím, co vidím. Je to kružnice.
.......
Offline
#14 13. 06. 2010 09:54 — Editoval zdenek1 (13. 06. 2010 10:01)
Re: Kružnice
↑ amater:
ad obrázek: Protože to bylo špatně.
Když umíš vypočítat vzdálenost dvou bodů, tak je to snad jasné.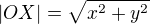 (O je počátek)
(O je počátek)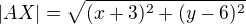
a podle zadání 
zbytek je algebra - umocníš a upravíš.
Edit: obrázek je takto:
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

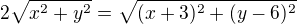

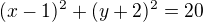
![kopírovat do textarea $S[1;-2]$](/mathtex/fd/fd75800a5b8e28ba05ee6b9408b736b1.gif) a poloměrem
a poloměrem