Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 13. 06. 2010 14:33
Re: Parabola
↑ amater:
Protože má parabola vrchol ![kopírovat do textarea $V[2;-1]$](/mathtex/ba/ba32b37de955c2a589ad987edc376301.gif) a parametr
a parametr  , je ohnisko
, je ohnisko ![kopírovat do textarea $F[4;-1]$](/mathtex/08/08b4cd465901742437e13720b15db95f.gif)
Všechny body vzdálené od ohniska 20 leží na kružnici 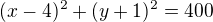
Průsečíky této kružnice a paraboly vypočítáme
 (druhý kořen nevyhovuje)
(druhý kořen nevyhovuje)
Dosazením za  do rovnice paraboly dostaneme
do rovnice paraboly dostaneme ![kopírovat do textarea $X_1[20;11]$](/mathtex/62/629364397a2c19711d1a56efc6962a82.gif) a
a ![kopírovat do textarea $X_2[20;-13]$](/mathtex/85/85f1a5803168d12eaf80a94aa166ef9e.gif)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#11 14. 06. 2010 11:05 — Editoval Cheop (14. 06. 2010 11:07)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Parabola
↑ sysellka: v intervalu
v intervalu 
Fce tg je:
I. kvadrant - kladná
II.kvadrant - záporná
III.kvadrant - kladná
iV.kvadrant - záporná
Ze zadání je jasné, že se jedná o IV. kvadrant.
Ve čtvrtém kvadrantu jsou fce:
sinus - záporný
kosinus - kladný
kotangens - záporný.


Nikdo není dokonalý
Offline
#12 14. 06. 2010 11:21
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Parabola
↑ sysellka:
IV. kvadrant:
sinus - záporný
kosinus - kladný
tangens - záporný
kotangens - záporný


Nikdo není dokonalý
Offline
