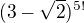Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 08. 10. 2010 18:31
Re: Vysoká mocnina výrazu a jeho sudost či lichost
Zdravím, vzhledem k tomu, že jde v podstatě o aktuální sedmou úlohu v PraSeti, navrhuji odložit odpověď až na úterý.
Offline
#3 08. 10. 2010 19:39
Re: Vysoká mocnina výrazu a jeho sudost či lichost
↑ Olin:
Zdravim:-) Jsi sikula, ze jsi si to vsiml ;-) Obdivuji ;-)
↑ Gustav;:
Pravidla jsou ti cizí? Tu se pomáhá těm, kteří něčemu nerozumí, nikoliv řeší soutěže. Soutěž je právě o tom, že se porovnávají schopnosti soutěžících, ne soutěžících, za které to vyřeší někdo jiný.
PRAVIDLA!!! 6. bod
"Vím, že nic nevím." Sokrates
Offline
#4 08. 10. 2010 19:46 — Editoval Olin (08. 10. 2010 19:48)
Re: Vysoká mocnina výrazu a jeho sudost či lichost
↑ b.r.o.z1:
Také zdravím, osobně bych nevolil tak ostré formulace, přece jen ctím presumpci neviny. Dokáži si dost dobře představit, že to nemá s prasetem nic společného a jde o náhodu.
Jinak vzhledem k tomu, že jsem byl jedním z lidí, kteří do této série úlohy vybírali, tak jsem to samozřejmě poznal :-) Jde o moc hezkou úlohu, která si právoplatně zaslouží být v sérii Triky.
Offline
#5 08. 10. 2010 22:24
Re: Vysoká mocnina výrazu a jeho sudost či lichost
Je fakt, že jsem právě PraSe řešil. Proto jsem ale nespal přesné zadání a ani nechtěl úplný postup. Soudím však, že jakákoliv pomoc by asi byla velkým spoilerem, takže se tímto omouvám.
Jsem vážně zvědavý jak to je. Už asi na nic nepřijdu.
Offline
#7 09. 10. 2010 10:54
Re: Vysoká mocnina výrazu a jeho sudost či lichost
Domnívám se, že uvedený vzorec platí pouze pro  (vzhledem k tomu, že na pravé straně je součet celých čísel, což je vždy celé číslo).
(vzhledem k tomu, že na pravé straně je součet celých čísel, což je vždy celé číslo).
Offline
#8 13. 10. 2010 00:44
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vysoká mocnina výrazu a jeho sudost či lichost
↑ Olin: Prozradíš myšlenku řešení? Pro PraSečí úlohu trik znám, zde mi jasný není (teda možná by šlo ten, kterým jsem řešil PraSečí úlohu, nějak rozšířit, ale nebylo by to moc pěkné).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 14. 10. 2010 22:17 — Editoval Olin (14. 10. 2010 22:17)
Re: Vysoká mocnina výrazu a jeho sudost či lichost
↑ Kondr:
Prozradím řešení původní úlohy - pro zadanou úlohu mě nic moc nenapadá.
Podstatou je uvědomit si, že čísla  a
a 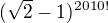 mají mnoho společného - totiž nejen že je jejich součin celé číslo (konkrétně jednička), ale dokonce i jejich součet je celé číslo - podle binomické věty totiž je
mají mnoho společného - totiž nejen že je jejich součin celé číslo (konkrétně jednička), ale dokonce i jejich součet je celé číslo - podle binomické věty totiž je
(označil jsem  ) a pokud tyto součty sečteme, odečtou se všechny členy, ve kterých je
) a pokud tyto součty sečteme, odečtou se všechny členy, ve kterých je 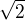 v liché mocnině, a ty se sudou mocninou (tedy celé) se naopak sečtou:
v liché mocnině, a ty se sudou mocninou (tedy celé) se naopak sečtou:
takže jde dokonce o sudé číslo. Avšak  , takže
, takže  . Odtud dostáváme, že
. Odtud dostáváme, že  . Zbývá si rozmyslet, že to nám již paritu
. Zbývá si rozmyslet, že to nám již paritu 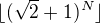 jednoznačně určuje.
jednoznačně určuje.
Offline
#10 15. 10. 2010 15:24
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vysoká mocnina výrazu a jeho sudost či lichost
Jo, uvažoval jsem v podstatě stejně:  je posloupnost daná vztahy
je posloupnost daná vztahy  ,
, 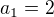 a
a 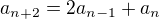 , tudíž je tvořena celými sudými čísly, posloupnost
, tudíž je tvořena celými sudými čísly, posloupnost 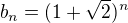 je pro sudá
je pro sudá  o nějaký drobný zlomek menší, po zaokrouhlení dolů tedy dává liché číslo.
o nějaký drobný zlomek menší, po zaokrouhlení dolů tedy dává liché číslo.
BRKOS - matematický korespondenční seminář pro střední školy
Offline