Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » Obvod a obsah pravoúhlého trojúhelníka (TOTO TÉMA JE VYŘEŠENÉ)
#2 11. 10. 2007 18:27 — Editoval Marian (11. 10. 2007 18:51)
Re: Obvod a obsah pravoúhlého trojúhelníka
Necht a, b oznacuji delky odvesen pravouhleho  . Oznacime-li pomoci c delku jeho prepony, pak plati
. Oznacime-li pomoci c delku jeho prepony, pak plati  , tzv. Pythagorova veta. Vyuzijeme to pozdeji. Z tveho zadani dale plyne, ze
, tzv. Pythagorova veta. Vyuzijeme to pozdeji. Z tveho zadani dale plyne, ze  (obvod) a
(obvod) a  (obsah). Od jednotek jsem pro jednoduchost abstrahoval. Mame tudiz dve rovnice:
(obsah). Od jednotek jsem pro jednoduchost abstrahoval. Mame tudiz dve rovnice:
a .
.
Z prvni z techto rovnic plyne  , (1)
, (1)
z druhe z nich pak (nasobili jsme ctverkou). (2)
(nasobili jsme ctverkou). (2)
Rovnici (1) umocnime na druhou, proto . (3)
. (3)
Vyraz 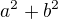 nahradime podle Pythagorovy vety vyrazem
nahradime podle Pythagorovy vety vyrazem  , vyraz
, vyraz  nahradime (jak jsme uvedli vyse v rovnici (2)) vyrazem
nahradime (jak jsme uvedli vyse v rovnici (2)) vyrazem  . Rovnice (3) dostava tedy tvar
. Rovnice (3) dostava tedy tvar .
.
Umocnenim na druhou a upravami dostaneme linearni rovnici ( se "pobije"):
se "pobije"): .
.
Jejim resenim je  , coz vyhovuje navic povaze ulohy. Dale je zapotrebi vypocitat delky odvesen. Dosazenim c=10 do rovnice (1) mame vztah
, coz vyhovuje navic povaze ulohy. Dale je zapotrebi vypocitat delky odvesen. Dosazenim c=10 do rovnice (1) mame vztah (4)
(4)
a z rovnice (2) vydelenim dvemi plyne . (5)
. (5)
Rovnice (4) a (5) musi platit soucasne a zaroven cisla "a" a "b" musi byt kladna. Tyto rovnice tvori soustavu dvou nelinearnich rovnic o dvou neznamych. Z rovnice (4) si napriklad vyjadrime neznamou "a": . (6)
. (6)
Toto dosadime do rovnice (5). Ta po dosazeni ma tento tvar: .
.
Jeji upravou pak mame .
.
Resenim posledni rovnice jsou cisla  a
a  . Nyni snadno dopocteme hodnotu
. Nyni snadno dopocteme hodnotu  , resp
, resp  a
a 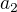 z rovnice (6). Proto
z rovnice (6). Proto  a
a  .
.
Takze vzhledem ke tvemu zadani existuji dva takove pravouhle 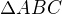 . Oznacim-li prvni z nich
. Oznacim-li prvni z nich  , pak mam
, pak mam  a pro druhy z nich, oznacme jej
a pro druhy z nich, oznacme jej  , plati
, plati  .
.
V podstate se jedna o jediny trojuhelnik, ale to je jiste videt (neprima shodnost).
Marian
=================================================================================
PS: Ted jsem si vsimnul, ze je to v sekci pro ZS. Ta uloha je spise pro stredni skoly, ale da se samozrejme resit i na ZS. Protoze jsem si teto skutecnosti nevsimnul, budou se pravdepodobne zdat nektere z uvedenych kroku v mem prispevku prilis rychle. Navic tedy to o neprime shodnosti ber v uvahu jako jiste preklopeni. Jestli budes mit nejake dotazy, pak jiste nekdo rad odpovi, protoze ja jsem na toto forum odskocil v rychlosti a resim podstatne hlubsi matematicke problemy, hlavne me tlaci jakysi termin.
Mnoho zdaru nejen v matematice.
M.
Offline
#4 15. 11. 2010 18:27
Offline
#5 15. 11. 2010 20:38 — Editoval Chrpa (15. 11. 2010 21:11)
Re: Obvod a obsah pravoúhlého trojúhelníka
↑ meďošek:
a)
Obvod: 
Případ b) obdobně
Mělo by ti vyjít: 
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » Obvod a obsah pravoúhlého trojúhelníka (TOTO TÉMA JE VYŘEŠENÉ)

