Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 10. 12. 2010 13:37
#5 11. 12. 2010 18:27
#6 11. 12. 2010 20:01 — Editoval lukaszh (11. 12. 2010 20:01)
Re: greenova věta
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 11. 12. 2010 20:12
#8 11. 12. 2010 22:00
Re: greenova věta
↑ Petik:
V prvom rade je zadané k zle. Chýba tam asi 
čo je rovnica elipsy. To, že nevieš, kam máš "dosadiť to k", tak to už nie je problém, ktorý by sa týkal tvojej pôvodnej otázky a pokiaľ nevieš riešiť integrál
tak sa treba spýtať v samostatnej téme. Podotýkam, že C je v tomto význame vnútro elipsy. Ale to už s Greenovym vzorcom nemá nič.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#9 05. 01. 2011 17:36
Re: greenova věta
↑ lukaszh:
a vies nam prosim ta poradit ze co s tou elipsou? ja mam napr presne rovnaky priklad a elipsa je kladne orientovana a z rovnice elipsy som ssi vyjadrila a=2, b=3. a neviem ako mam dosadit hranice integralov ci nejako parametricky vyjadrit alebo mozem na osi x od 0 po 2 a os y O-3 ? dikes
Offline
#11 05. 01. 2011 22:20
Re: greenova věta
 ↑ lukaszh:
↑ lukaszh:
inak pocuj to na zaciatku si mohol to minus pred zatvorkou B integralu roznasobit so zatvorkou ? a ako si dostal to ró a t? tam musis dosadit take hodnoty aby X bolo 2 a y 3? a co je ten jakobian googlim googlim ale nejde mi to do hlavy
Offline
#12 05. 01. 2011 22:49 — Editoval lukaszh (05. 01. 2011 22:51)
Re: greenova věta
↑ Atima:
Mám tu pár ponaučení:
Základná škola
--------------------------
Áno, môže sa to. Totiž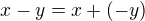
Stredná/Vysoká škola
--------------------------
No neviem, ja poznám takéto prevody súradníc zo strednej školy. Odporúčam zopakovať. Tu je niečo k polárnym súradniciam.
Vysoká škola
A čože je to za školu, kde od vás chcú počítať integrály substitúciou bez znalosti Jakobiánu? Jakobián toho zobrazenia je
EDIT: Ešte odporúčam prezrieť materiál http://homel.vsb.cz/~kuc14/VKM/prez/vkm_pr07.pdf
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#14 06. 01. 2011 12:19
Re: greenova věta
↑ lukaszh:este sa ta mozem spytat? potom ked uz idem riesit ten dvojny integral tak uz zadam len to 6ro namiesto jakobianu? ci este mam tou dvojkou roznasobit tie polarne suradnice ? diks
tak uz zadam len to 6ro namiesto jakobianu? ci este mam tou dvojkou roznasobit tie polarne suradnice ? diks
Offline
#16 07. 01. 2011 20:43
#17 08. 01. 2011 19:46
Re: greenova věta
↑ lukaszh:
lukas vies mi este pomoct s intervalom T pri parabole? tiez tam ma byt (0,1) ako pri useckach? alebo ako pri napr kruznici? diks
Offline




![kopírovat do textarea $x(t,\rho)=2\rho\cdot\cos(t)\nly(t,\rho)=3\rho\cdot\sin(t)\nl\rho\in[0,1],t\in[0,2\pi)$](/mathtex/ca/ca6f449231ddc1083bff739a7748f7e9.gif)
![kopírovat do textarea $\cdots=\int_{0}^{1}\int_0^{2\pi}-2\cdot 6\rho\,\rm{d}\rho\rm{d}t=\int_{0}^{1}\left[\int_0^{2\pi}-12\rho\,\rm{d}t\right]\rm{d}\rho=\cdots$](/mathtex/01/01ef7a6a7083fe098a368fdd68b1cfec.gif)