Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 05. 2011 19:42
komplexni cislo
Dobry vecer, potreboval bych poradit s timhle prikladem: V oboru komplexnich cisel reste kvadraticke rovnice x^2 -4 =0. Jejich reseni vyjadrete v goniometrickem tvaru.
Vypocital jsem x1= 2i a x2= -2i. Jak ted vyjadrim v goniometrickem tvaru, kdyz nevim kolik se rovna realny cast k. c. ?
Učený hlupák je větší hlupák než hlupák nevzdělaný.
Offline
- (téma jako vyřešené označil(a) Asqwer)
#2 06. 05. 2011 19:45 — Editoval Phate (07. 05. 2011 12:05)
Re: komplexni cislo
pokud je zadani  :
:
Edit: je ta rovnice spravne takto? ta rovnice ma realne koreny a ne komplexni
protoze diskriminant vychazi 4 a koreny jsou

Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#7 06. 05. 2011 20:06 — Editoval Dana1 (06. 05. 2011 20:35)
- Dana1
- Host
Re: komplexni cislo
↑ Asqwer:
Neviem, ale pochybujem.
Proste 2i je rýdzo imaginárne komplexné číslo - a takéto číslo má reálnu časť rovnú nule. Znázorni si to v komplexnej rovine a hneď uvidíš aj uhol...
Možno pomôže toto, konkrétne asi operácie s komplexnými číslami a goniometrický tvar komplexného čísla...
Dokonca je tam na strane 5 úloha 5 v časti Goniometrický tvar komplexného čísla I riešená presne Tvoja úloha.
#11 07. 05. 2011 14:23 — Editoval ALDRED (07. 05. 2011 14:25)
Re: komplexni cislo
kdyz mam treba rovnice a.x^2 + b.x +c= 0, tak cislo b je realna cast k.c ?
Pokud mas rovnici 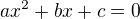 a tato rovnice ma pouze komplexni koreny, tak realna cast se rovna
a tato rovnice ma pouze komplexni koreny, tak realna cast se rovna  (jde to videt dobre z tvaru pro vypocet korenu:
(jde to videt dobre z tvaru pro vypocet korenu:  ). Ale neprijde mi to nijak dulezite si to pamatovat jako nejakou specialni vlastnost, protoze to s trochou zamysleni vzdy odvodis :)
). Ale neprijde mi to nijak dulezite si to pamatovat jako nejakou specialni vlastnost, protoze to s trochou zamysleni vzdy odvodis :)
Offline
#13 07. 05. 2011 14:36
Re: komplexni cislo
↑ o.neill:
Asi jsem zapomnel doplnit, ze predpokladame rovnici s realnymi koeficienty, ze? :)
Offline

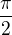 pro 2i a
pro 2i a 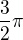 pro -2i
pro -2i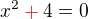
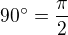 ?
?